Hector Parr's Home Page

App3.01 Much thought has been given in recent years to the design of the next generation of digital computers, and to the possibility of building machines which make direct use of the quantum properties of elementary particles. Some of the work currently being done in this field has direct relevence to the validity of the nodal hypothesis, and so we must enquire how it impinges on nodal theory, whether its discoveries might suggest modifications to the theory, or whether indeed the nodal hypothesis could become untenable if this work eventually succeeds.

App3.02 If such a quantum computer can ever be built, it will have some obvious advantages over today's machines. The last twenty years have seen a steady and remarkable increase in the power of digital computer systems; both the memory capacity and the processor speed of the small personal computers which can be bought for between £1000 and £2000 have practically doubled every two years, resulting in an increase of both these characteristics over the twenty year period by a factor of about one thousand. Alongside the increasing speed there has been a steady advance in the miniaturisation of components, so that today's computers are still about the same size as those of twenty years ago, despite their enormously increased power. These two attributes, size and speed, are of course related, and every increase in clock speed sees a decrease in the distance which signals can move, even at the speed of light, during one clock cycle. At the time of writing, clock speeds in the region of 1 GHz are common, so that in the duration of one cycle a signal can move no further than about 30 cm, and parts of a machine which are synchronised to the clock-pulses must lie within a very few centimetres of each other. We can expect this process of miniaturisation and increasing speed to continue for several more years, but we shall eventually reach a natural limit where the number of electrons comprising the signal currents will be too small to allow reliable operation. Clearly this barrier can be breached if individual molecules, atoms or sub-atomic particles themselves become the devices which store and operate on the bits of data which a computation requires to be handled, and this promise of smaller and faster devices provides one incentive for the development of components which function at the atomic level.

App3.03 An essential building block of the conventional computer memory is the bi-stable, a tiny electrical circuit that at any moment can display only one of two clearly defined states, and so can store a 0 or a 1, as required in handling binary arithmetic. In today's computers a register often consists of 32 bi-stables, and so the whole register can store in binary form any integer between 0 and 2³² - 1, a total of about four billion possible integers. At least in theory, the world of atomic particles can supply us with unlimited "bi-stables", for many elementary particles possess an intrinsic "spin" and a magnetic moment, and whenever an attempt is made to determine whether the spin axis lies along a particular direction the answer is always just "yes" or "no". Under certain conditions a single particle can preserve its spin between one measurement and the next, and so can act as a ready-made bi-stable for storing a binary digit. The possibility of building a quantum computer using single elementary particles in place of electronic bi-stable circuits is currently being investigated at several research centres around the world.

App3.04 But what has caused the greatest excitement is the belief held by some physicists that a quantum computer, in addition to its increased speed and storage capacity, would permit the processing of vast amounts of data in parallel and simultaneously. In a traditional computer, when large numbers of data items are to undergo the same operation, as in many arithmetic procedures, this operation must be repeated successively as many times as necessary. If speed is vitally important, the only alternative is to use a large number of separate processors working simultaneously in parallel. Many physicists believe, however, that a quantum system can exist in a superposition of states, and does not collapse onto a recognisable state unless it is observed or measured. So whereas a traditional computer memory register can hold only one number at a time, a quantum register could hold simultaneously all the numbers of which it is capable. Furthermore, all these numbers can be processed together in one operation, provided we do not observe it until the task is completed. This parallelism is far more powerful than may be apparent at first sight. A conventional 32-bit register can hold at any moment of time just one of the four billion numbers of which it is capable, but if this could be implemented by 32 two-state quantum units, then between one measurement and the next this quantum register could be in a superposition of all its four billion states, and could store simultaneously four billion different numbers. If these all required the same operation performed on them this could be implemented instantaneously in parallel. It is easy to understand the enthusiasm of those currently working in the field of quantum computing.

App3.05 For many mundane purposes the speed of such a quantum computer would be of little advantage, for it would not provide a noticeable improvement over a conventional machine. But some apparently simple tasks seem incapable of solution on today's computers in a reasonable time because of the vast number of repetitive operations needed. If you are asked to add together two ten-digit numbers with paper and pencil, this will require just ten additions. If you need to multiply together two such numbers you will have to do one hundred multiplications. We say the complexity of adding together two m-digit numbers is of order m, and of multiplying together two m-digit numbers is of order m². In both cases the process can be performed by a computer in polynomial time, for m and m² are both polynomials. But some calculations cannot be performed in polynomial time; their complexity may be, for example, of order 10^m, which for sufficiently large m will require a much greater time than any polynomial function you can write down. Such processes are said to need exponential time, and it is for this class of calculation that the quantum computer, if it can ever be built, would prove invaluable, for it could reduce some exponential time problems to polynomial time.

App3.06 One notable example of such a problem is the factorisation of large numbers. Without using your calculator or computer, can you find the factors of 9,881,383 ? However good your paper-and-pencil arithmetic, this problem would probably occupy you for several days; factorisation requires exponential time. But interestingly the reverse problem, of forming a number when its factors are known, requires only polynomial time, and is far less complex. Try multiplying together 2657 and 3719. This should take you no more than about one minute, and the product is, in fact, 9,881,383. No doubt a conventional computer could factorise this number in a second or two, but one with a hundred digits rather than seven might take it hundreds of years. The virtual impossibility of factorising large numbers is the basis of some modern cryptography. The codes that are used to transmit sensitive financial data often rely upon this fact, and would be vulnerable if a new generation of computer were able to accomplish such factorisations in a reasonable time.

App3.07 Never has the gulf between theory and practice been so wide. At the time of writing (2002) very little practical work has been carried out that can reasonably be called "quantum computing". One approach is described in a paper by Matthias Steffen et.al. of Stanford University, (Toward Quantum Computation, IEEE, 2001). They have developed a substance whose molecules include five fluorine atoms, and each atomic nucleus displays one unit of spin. They dissolved this substance in a liquid and placed a sample in a Nuclear Magnetic Resonance machine. By subjecting these molecules to magnetic pulses of carefully chosen frequency and duration they were able to control and measure the spins of the five fluorine nuclei individually, and they claim to have created a computer with two registers, one of two bits and one of three, capable of holding any integer from 0 to 7. (They were, of course, manipulating a large number of molecules in parallel. But this is not the essential parallelism of quantum computing, which was represented by the superposition of states of the atomic nuclei in each individual molecule.)

App3.08 Experimental work is being performed elsewhere, but as yet it is all on this same minimal scale. This contrasts with the considerable amount of theoretical work being done at many different centres around the world, devising tasks suitable for quantum computer solution, designing on paper the necessary logic gates, devising possible computer architectures, and writing code for the actual programs to run on quantum computers which as yet exist only in the imagination. Some of these tasks will demand registers comprising hundreds or thousands of quantum two-state units, and no-one knows of what these will consist, or whether they will work. It is acknowledged that a major hurdle to overcome will be "decoherence", the collapse of a particle's wave form whenever it reacts in any way with its surroundings, and the consequent loss of any information it may be carrying, whether or not this is part of a "superposition" of data. But there will undoubtedly be many other problems, some of which have not yet been conceived.

App3.09 A significant advance was made in 1994 when Peter W. Shor published details of an algorithm which he claims will enable quantum computers to factorise numbers in polynomial time, and so permit the factorisation of numbers far larger than any traditional computers can manage (Polynomial-time Algorithms for Prime Factorisation, IEEE Computer Society Press). The machine will require two quantum registers, which we shall call A and B, and the total number of bi-stables needed will be no more than about ten times the number of digits in the number we wish to factorise, which we call n. The number in register A at any moment we shall call a, and that in B is called b. The process can be divided into three parts, which we describe in some detail in an attempt to assess its feasibility.

App3.10 Firstly each element of register A is put into an equal superposition of its two possible states, so that the register as a whole is in an equal superposition of every possible number it can contain. As explained earlier, this could be a vast number; if n has about 80 digits, the number of possible values of a would exceed the number of particles in the universe, but these are all supposed to exist simultaneously in superposition. A small number x is then chosen almost at random, and Register A is subjected to a quantum process which puts into register B the following function of the number a:

App3.11 For the non-mathematician a simple example will show what this means. Let us take n = 91 (obviously ridiculously small, but sufficient for illustration), and x = 3. Each value of b is the remainder when x^a is divided by n, and the following table shows this for the first few values of a.

        a               xa              b
       ----------------------------------
	0		1		1
	1		3		3
	2		9		9
	3		27		27
	4		81		81
	5		243		61
	6		729		1
	7		2187		3
	8		6561		9

It will be seen that the values of b are forming a sequence which repeats itself after every 6 values, and this continues for all values of a. We call 6 the period of the sequence, and denote it by r. In a real application of the method, r might be a very large number. Shor explains that register B then contains a superposition of all these values of b, just as A contains a superposition of all possible values of a. What we want to know is the value of r, the period of the b sequence, for it is easy to find at least one factor of n if the value of r is known (provided r is an even number; if not we can try again with a different value for x).

If you want the mathematics:

r is the first non-zero value of a for which x^r = 1 (mod n)
So x^r = mn + 1 where m is some whole number.
So x^r - 1 = mn
So (x^r/2 - 1)(x^r/2 + 1) = mn
It follows that at least one of (x^r/2 - 1) and ( x^r/2 + 1) must have a factor in common with n .

App3.12 If we now observe register B, standard quantum theory decrees that its contents must collapse at random to one of its possible values (in our little example, perhaps to 9). But furthermore, because the registers are entangled by the quantum process which calculates the b values, register A must collapse also, but only to those values which make this b value possible, and so a now contains a superposition of this restricted set of a values (in our example, 2, 8, 14, 20, etc.).

App3.13 In the example it is clear on inspection that the value of r is 6, but if r lay in the millions or billions its value would not be so obvious. So Shor now applies another process to the superposition of a values, and finds their discrete Fourier transform, a process that can be done in a quantum computer using a method devised by D. Coppersmith (An approximate Fourier transform, IBM Research Report RC19642 (1994)). In effect this transformation replaces the (restricted) set of a values by their spectrum in the same way that a spectroscope analyses light of different wavelengths into a spectrum of bright coloured lines, or an acoustical spectrum analyser splits up a sound wave into its component harmonics. If we now observe the A register it will collapse to indicate a randomly selected one of the "harmonics", and if we repeat the whole process several times and record the values we obtain, it will be clear that all are multiples of some fundamental frequency, from which we can find the period of the original b values, or r. This gives us at least one of the factors of n as explained above, and we can then reduce the complexity of the problem by dividing n by these factors. It may now be possible to find the other factors using a conventional computer. If not, we can employ once again our quantum computer to reduce the problem a stage further, until we have found all the factors of n.

App3.14 Now what contribution can the Nodal Theory make to this new discipline? It will certainly ask for some of the speculative precedures being investigated by workers in this field to be described in somewhat different terms from those at present in use. But will it help to assess whether quantum computers can ever be built, and if so how useful they are likely to be?

App3.15 The essence of all these quantum methods lies in the manipulation of wave functions of superpositions, such as that described above. This manipulation must necessarily remain hidden from view, for conventional quantum theory tells us that the wave function of a system collapses to a single state whenever we observe that system. But Nodal theory adopts a different view. It maintains that these wave functions have no real physical existence, for they must belong to the class we have called conventional wave functions (CWF) and not to the class of nodal wave functions (NWF), as defined in Chapter 5. This classification is demanded by the strong time-asymmetry of the collapsing waves; any NWF must be totally time-symmetric. Thus the CWF represents only the constructions we ourselves create in our attempts to predict the future behaviour of a system which we cannot know for certain because our knowledge is always restricted to the past. When we describe a system as being in a superposition of different states, and assign quantum amplitudes to each state, nodal theory asserts that these amplitudes merely indicate the (complex) probability that such a state will be found to occur when we subsequently observe the outcome, a probability that may well be personal, in the sense that different people with different knowledge of the system's past history can quite properly assign different amplitudes to the same state. Only one outcome actually occurs, and to nature herself all the others mean nothing; they are significant to us just because in our ignorance we believe they might possibly come about. So when we describe a system as being a superposition of states, each with its own probability of being realised, the system is really in just one of those states, moving towards the outcome which eventually is realised. All the other states represented in the superposition exist only in our minds.

App3.16 Let us examine the first stage of the Shor process from the two viewpoints, that of quantum theory as conceived by Shor and his colleagues, and that of nodal theory. The binary number a, contained in Register A, is acted upon by the function-generating hardware that calculates the value of x^a(mod n) , and this number is stored in register B. The conventional view is that A is in a superposition of states in which it contains every one of the numbers of which it is capable, these are simultaneously processed by the function generator, and then register B is in a superposition of states corresponding to all the numbers that can result from such a calculation. Then when we look at B its waveform collapses and we observe just one value of b, chosen at random from these possible values. What is the Nodal description of the process? In its original state, Register A contains just one value a, and this one number is processed by the function-generator and put into register B. Then when we look at register B we see just this one value of b, chosen at random from the possible values. We see that the conventional viewpoint and the nodal viewpoint describe the process very differently, but both appear to describe the observed outcome equally well.

App3.17 But in the next stage of Shor's process the nodal theory scores the advantage, for the conventional view has to explain how, when we observe B and collapse its wave-form, this collapse is somehow transmitted backwards into register A. A is supposed still to contain a superposition of a values, but only that reduced set which are consistent with the value of b which we observed in register B. On the other hand the nodal viewpoint has nothing to explain, for A only ever contained one value, and this value was responsible for the number in B which we observed.

App3.18 The third stage, the replacement of a in register A by the result of applying a Fourier transform to a, shows up the real difference between the two theories. According to Shor's theory A contains a superposed set of values for a, and the Fourier transformation should reveal a sort of "line spectrum" for this repetitive series, from which the period r of the series can be found. But the nodal theory insists that A can contain only one value; applying Fourier to this does not achieve very much, but if the process worked at all it would generate a continuous spectrum. When we come to observe the final value in the A register we are as likely to obtain any one value as any other; it will tell us nothing. So Nodal theory predicts that Shor's method, despite its ingenuity, will not work.

App3.19 What exactly does this mean? At first sight it may seem that, when we build our first machine to apply the Shor method, we shall be able to distinguish between the two theories. If the machine works then conventional quantum theory is vindicated. If it does not then it is condemned, and the nodal theory, while not proven, is still in the running. But the situation is not as simple as this. We have maintained throughout this treatise that the Nodal theory does not tell us anything about the results of experiments or observations; it is concerned only with reasons and interpretations. So the success or failure of a quantum computer can neither support nor refute nodal principles; it can not decide between nodal theory and mainstream quantum theory.

App3.20 The writer believes, however, that Shor's method, along with the work of several others doing research in the field of quantum computing, do not represent mainstream quantum thinking. The essential feature of all proposed schemes is the possibility of putting a system into a superposition of states, and of preserving this superposition through a number of processes. The avowed belief seems to be that unless someone observes the system then the waveform does not collapse. Perhaps the most familiar example of such a system is provided in the well-known legend of Schrodinger's cat, which we mentioned in Chapter 12. When the moment comes for the fateful nucleus to divide, or not to divide, as the case may be, it is put into a superposition of two states, with very different consequences. Then these two chains of consequences are supposed to co-exist until the moment the box is opened. If no-one looks inside for one hour, then the dead cat and the live cat must have co-existed in superposition for this length of time. Now the writer does not think a majority of physicists really believe this, and they are in good company, for it was Niels Bohr himself who declared that the collapse of the waveform occurs not just when someone "looks", but as soon as any "irreversible amplification" takes place. The shattering of a flask of poison is certainly irreversible, and is also an amplification of the splitting of a single atom, so the superposition must have collapsed long before the cat dies (or not, as the case may be). The nodal theory is more specific, and declares that in general the waveform of a particle collapses as soon as it reaches its next node. (The only exceptions are in situations like reflection from a rigid mirror, when the wave gives up only a small part of the information it carries, and is able to go on to the following node sufficiently intact to cause interference effects there, as described in Chapter 7.)

App3.21 In the final stage of any successful implementation of Shor's algorithm the set of numbers superposed in the A register is subject to a Fourier transformation. Shor summarises this process by quoting the mathematical operator which gives the final state of the A register in terms of its previous state, as follows (where q is the total number of possible a values):

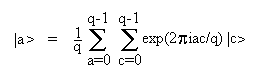
App3.22 It will be seen that each of the superposed numbers must be multiplied by every other number in the superposition. This requires each bit of each number being accessed a large number of times, sometimes being found to contain a "1" and sometimes a "0", and this information is used to influence that part of the system which is summing the results of these multiplications. It seems certain that both mainstream quantum theory and the nodal theory deny the possibility of this happening. Standard quantum theory acknowledges that a particle in a superposition of states can give up its information once only, after which it will give the same value each time it is measured. For example, a photon which has been transmitted by a polaroid filter will be transmitted by any other such filter whose axis is parallel to that of the first. Both mainstream quantum theory and the nodal theory thus declare that such a quantum computer, relying on the simultaneous processing of a superposition of states, will not perform as required. Only the more extreme interpretations of Shor and his colleagues provide any basis for a belief that it will.

App3.23 So what are our conclusions? If such a parallel quantum computer is ever built, and if it ever functions as intended, then these extreme beliefs will be supported, and the future for computing will be exciting indeed. The traditional quantum theory of Bohr, Feynman and their conservative colleagues will have to be discounted, and the Nodal theory also must be consigned to the flames. The most secure coding systems used by the world's banks for transmitting sensitive information will become assailable, and a large part of the literature on quantum theory will have to be rewritten. But the writer is confident that this will not come about. Those presently engaged in the quest for a new species of quantum super-computer, for which they must believe that quantum superpositions can survive despite their internal interactions, will be shown to have backed the wrong horse. Mainstream quantum theory and the Nodal theory will remain as viable alternatives, and will be free to compete on the only playing field that is open to them, the field of plausibility.

Previous  Next  Home                    Hector Parr's Home Page