Ch. 1
Ch. 2
Ch. 3
Ch. 4
Ch. 5
Ch. 6
Ch. 7
Ch. 8
Ch. 9
Ch.10
Ch.11
Ch.12
App.1
App.2
App.3
Biblio.
Index
Hector Parr's Home Page
Quantum Physics: The Nodal Theory
Hector C. Parr
Chapter 10: The Special Theory of Relativity
10.02 Towards the end of the nineteenth century there was much discussion on whether it is meaningful to talk about absolute states of rest and motion, or whether the only sort of motion that makes sense is relative motion. In everyday life we think of trains and aircraft as moving, and houses and mountains as stationary, but when challenged we are ready to acknowledge that nothing on the earth's surface is really motionless. Our houses are moving at several hundred miles per hour because of the earth's rotation, and the earth itself moves at almost 70,000 mph in its annual journey around the sun. The sun has its own motion within the galaxy, and the galaxy also moves within the group. Is all motion relative? Can we not discuss the motion of something in relation to space itself?
10.03 Numerous methods exist for measuring the speed of light in empty space, and to a high degree of accuracy these all give the same result, which is close to 186,000 miles per second. But what does this mean? Is this an absolute speed or is it relative to something else, and if so, what? There are only three possibilities. Those who believe that all motion is relative might tell us either (i) that the speed of light always has the same value in relation to the source of the light waves, or (ii) that this constant speed is relative to the observer of the light, or the object on which it falls. On the other hand those who claim that absolute motion is meaningful need not specify to what the motion of light is relative; they tell us (iii) that light moves at 186,000 miles per second relative to space. As the nineteenth century physicists wrestled with this question they were baffled to find that each one of these three possibilities led to contradictions. Let us now examine each of them.
10.04 The first theory, that light always travels at the same speed relative to its source, is easily dismissed. Astronomers have discovered very many double stars, pairs of stars which revolve around each other, often taking no more than a few days to complete each revolution. So for part of the journey a star can be moving towards the earth, and for another part away from the earth. The light from some of these stars has travelled for many years before reaching us, and if its speed were related to that of the star which emitted it, we would observe some strange effects indeed. The light originating from the star as it moves towards the earth would eventually overtake that emitted a few days previously as it moved away from us; we would sometimes see the star in several positions at the same time, and sometimes we would not see it at all. Such weird effects are never observed, so we can rule out the first of our three suggestions.
10.05 The second possibility, that the speed of light is constant relative to its observer, also seemed to pose contradictions.Suppose you are at rest relative to a nearby beacon, and you are measuring the speed of the light which reaches you from the beacon. Then, while continuing to measure the light's speed, you set off in a car and travel away from the light source at 60 mph. After one minute you will be one mile further from the beacon, and its light will be taking an additional 1/186,000 second to reach you. So during the time you were travelling, the light must have been passing you at less than its usual speed; this second possibility also seems to be wrong.
10.06 It was the third suggestion that was favoured by most scientists in the 1880's and 90's. They believed that light waves had much in common with sound waves, and just as sound consisted of disturbances in the air, and travelled at a constant speed relative to the air, so light was supposed to consist of disturbances in some kind of ether, and the speed of light was constant relative to this ether. There was much debate on whether the ether around solid bodies such as the earth and the moon was dragged around with them as they moved, or whether it just flowed through them undisturbed. The first of these proposals was ruled out when it was found that, as the moon moved over a distant star during an occultation, there was no disturbance to the apparent position of the star right up to the moment of its disappearance, for this implied that the ether near the moon's surface was not being moved along by the moon's motion. The second proposal, that the ether passed through a moving body just as if it were not there, could be tested by experiments on the earth's surface, for then there would be an ether "wind" blowing through the earth, just as a traveller in an open vehicle experiences a wind on his face, and this would result in light having different velocities in different directions. The most famous and the most successful of the experiments to detect the ether wind was carried out by Albert Michelson and Edward Morley in 1887. In effect they compared very accurately the speed of a light ray traversing their apparatus in a North-South direction with one moving in an East-West direction. They then turned the whole experiment through 90o, expecting that this would change the timings if an ether wind were passing through the labaratory, but no change at all was detected. Just in case they had, by coincidence, performed the experiment on the very day that the earth happened to be stationary in relation to the ether, they repeated it six months later. Once again no trace of ether wind was found. We seem to have ruled out all three of our possible assumptions.
10.07 To overcome such complete deadlock
demanded extreme measures and clear thinking, and much credit is due to
H. A. Lorentz (1853 - 1928) for laying the foundations which eventually
showed us the way out of the impasse. Lorentz attempted to reconcile
the second and third of the above suggestions. He retained a belief in
the universal ether, but believed it might still be possible for every
observer to find the same value for the speed of light, whatever his
state of motion, if this motion itself affected the process of
measurement in some way. He proposed that the equipment with which the
moving observer measured the light's speed might contract
slightly along the direction of his motion. But this contraction would
not be noticed by the observer himself, for if he tried to measure the
length of the apparatus he would need some sort of ruler to do so, and
this ruler also would contract in the same ratio. Even the observer,
and the width of his eyeball, would contract to this same extent, and
so as far as he is concerned, no contraction occurs. But to the
stationary observer, if he had some clever way of accurately measuring
the moving ruler, the contraction would be apparent. In order to get
the right answers, Lorentz maintained that not only the moving
observer's measurements of length are affected, but his measurement of time intervals
would also be changed, and the two inaccuracies would combine to give
just the right value for the speed of light, measured in any direction.
Lorentz declared that if we observe anything which is moving relative to ourselves, then all distances along the direction of motion appear to suffer this Lorentz contraction, and anything which can measure time on the moving body appears to experience this time dilation.
These effects are not quite as unreasonable as may at first be thought,
for matter was known to contain electrically charged particles, and it
was possible that these would be affected by the ether wind when an
observer was in motion.
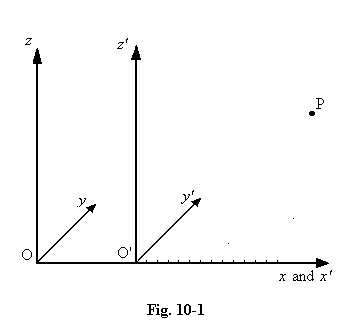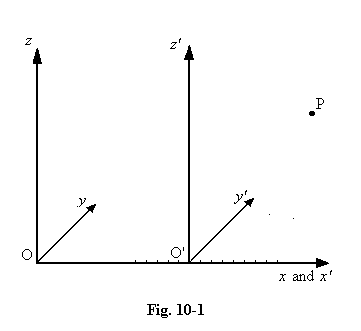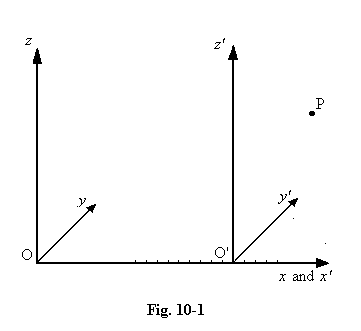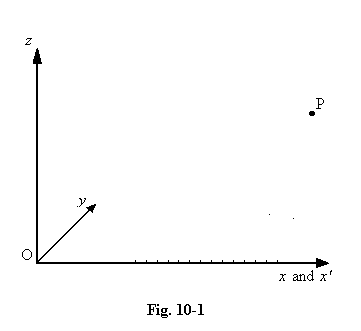
10.08 The Lorentz effect is illustrated in the above animation. Suppose O is an observer whom we consider to be stationary, and Ox, Oy and Oz are a set of co-ordinate axes he sets up in order to specify the position of any point in space, such as P, which we suppose to be fixed at the point (x, y, z). O' is a second observer who is moving along the x-axis with speed v, and O'x', O'y' and O'z' are the axes which he carries along with him. It is clear that the two observers will agree on the y and z values of the point P, for there is no relative movement in these directions, but the x'-value of P, as observed by O', will be constantly changing because of the relative motion. If t is the elapsed time since O and O' coincided, then (before Lorentz had proposed his new theory) we would have expected the following relationships to apply :

The fourth of these equations is inserted because it seems obvious that the two observers will agree on what time it is. But now Lorentz teaches us that:
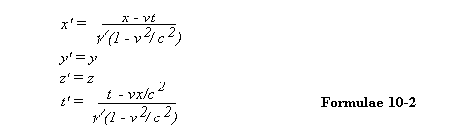
where c stands for the speed of light. These formulae show the manner in which measurements of length and time differ between two observers who are in relative motion to each other, and these differences do remove the paradox concerning the speed of light.
10.09 To see how the Lorentz formulae describe the contraction of a measuring rod when viewed by a moving observer, suppose the stationary observer is holding the rod parallel to his x-axis, and that the moving observer attempts to measure its length as he passes. To the stationary observer the length of the rod is the difference between the x-co-ordinate of its two ends, namely x2 - x1. But the length of the rod as seen by the moving observer would be x2' - x1'. Using the above formulae it is easily shown that the latter result is less than the former. The length as viewed from the moving reference frame is less than that in the stationary frame, assuming, of course, that each observer looks at the two ends of the rod at what he considers to be the same instant of time (and makes due allowance for the finite speed of the light rays by which he sees them).
10.10 This
is such an unexpected result that one may ask why it was not discovered
experimentally long ago. The reason is simply that all the velocities
with which we deal in everyday life are much less than c, the velocity of light, and the formulae show that the contraction effect is then very small indeed. If v
is 5 miles per second, about the speed of an orbiting earth satellite,
the contraction is less than one part in a thousand million; but it
becomes more significant as v approaches the value of c, and theoretically an object's length would vanish completely if it could reach the speed of light.
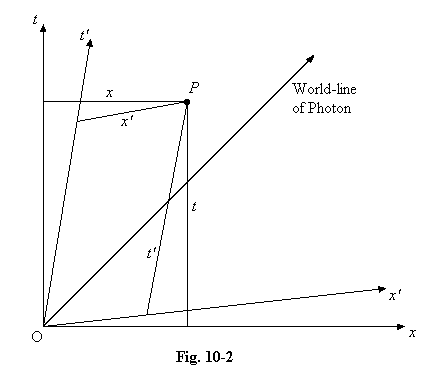
10.11 It is instructive to view the relationship between the two reference frames on a diagram which shows the time co-ordinate as well as the spatial co-ordinates, as we did in Chapter 2. We can visualise no more than three axes, and so must abandon one or more of the space co-ordinates, and in fact on this diagram we ignore both the y and z co-ordinates, but this does still allow us to see the important relationships between the x's and the t's. The t axis represents the world-line of the stationary observer, and the t' axis that of an observer moving with speed v along the x-axis. The Lorentz equations show us that Ox', the x-axis for the moving observer, no longer coincides with Ox, the stationary observer's x-axis. Furthermore, the x' axis can no longer be drawn at right angles to the t' axis, and in fact as v increases both these axes move towards the line we have drawn at 45o representing the world line of a photon or a flash of light. Recall that v can never exceed c. We show an event P, and draw lines to indicate its co-ordinates in both systems. The diagram also shows clearly a fact we stressed in Chapter 2, that the notion of simultaneity is purely subjective. The x-axis represents all those events which a stationary observer at O regards as simultaneous, for every point on the x-axis has a t-value of 0. But to the moving observer at O, it is the x' axis which represents the events for which t' = 0, and so these are the events which this observer regards as simultaneous.
10.12 But our troubles are not yet over, for several other physical formulae are not transferred correctly by the Lorentz transformations, including all the well-known formulae of mechanics. And there was something unsatisfactory about Lorentz's theory. It claims that there is a state of absolute rest, but that nature goes to great lengths to hide it from us. This contraction of measuring rods and slowing down of clocks is cleverly contrived to prevent us ever knowing whether something is truly motionless, or whether a relative speed is really the true absolute speed. Such a conspiracy would be difficult to explain or believe.
10.13 It was at this point that Einstein
came onto the scene, and he tackled the problems in a much more
thoroughgoing way than anyone before him, and took as his Principle of Relativity the following doctrine:
If K and K' are any two co-ordinate systems, and K' moves relative to K at uniform speed and without rotation, then all the general laws of physics take exactly the same form in K' as in K.Basing his calculations only on this one principle Einstein resolved all the outstanding problems with his Special Theory of Relativity. The principle does rule out the possibility of an absolute standard of rest, for this would single out one particular co-ordinate system. But Einstein showed that the Lorentz effects did not, after all, require the existence of the ether, and he made them seem much more plausible by showing that the contraction and time dilation were not real physical changes, but just appeared naturally because of the different systems of measurement used by the two observers.
10.14 Perhaps the most noteworthy of Einstein's conclusions concerns the notions of mass and energy.
He show us that the mass of an object is not a constant, as had always
previously been thought, but must be considered to increase as the
object's speed increases. We shall use the symbol mo to represent the body's rest-mass, and we find that the actual mass at speed v is given by:
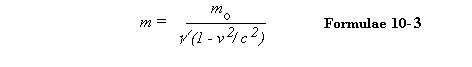
Einstein teaches us that mass and energy are really manifestations of the same characteristic of a body, and that a body must be considered to contain energy even when it is not moving. The rest-energy of a body is found to be

and the total energy of a moving body, including its kinetic energy, is given by
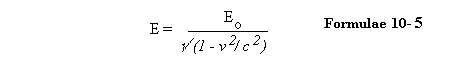
This leads us to the best-known of all the formulae of Special Relativity,

where m is the total mass of a body as given by formula 10-3 above.
Calculations show that the classical textbook formula for the kinetic energy of a moving object, K = mv2/2, is not accurate at high speeds, whether or not the value of m takes account of Einstein's formula 10-3. We can find the true value by subtracting Eo from E, and for values of v not too near to c the result can be expressed approximately as follows:
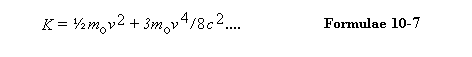
The only other result required in our treatment of the Nodal Theory is the formula for the momentum of a body. This is given in relativity theory, as it is in classical theory, by

but care must be taken to use the correct value of m, and not mo.
10.15 The writer regrets it is has been necessary to treat Einstein's theory so cursorily, but a fuller treatment would have been out of place in a book on Quantum Theory. He does hope that readers who have not studied this beautiful branch of physics will explore it further in other books or web pages.
(c) Hector C. Parr (2002)
Previous Next Home Hector Parr's Home Page