Ch. 1
Ch. 2
Ch. 3
Ch. 4
Ch. 5
Ch. 6
Ch. 7
Ch. 8
Ch. 9
Ch.10
Ch.11
Ch.12
App.1
App.2
App.3
Biblio.
Index
Hector Parr's Home Page
Quantum Physics: The Nodal Theory
Hector C. Parr
Chapter 6: Interference
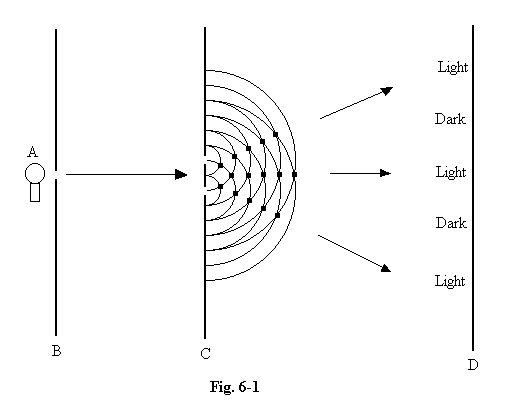
6.02 By modern standards this is an easy experiment to repeat, and it seems to be just as easy to explain. But quantum mechanics has destroyed this apparently simple explanation, highlighting several of the most subtle problems which quantum theory has to face. That is why every elementary book on quantum mechanics devotes space to describing Young’s experiment, and why we dedicate a chapter to it here.
6.03 After Louis de Broglie had suggested that particles of matter such as electrons might also display the same particle-wave duality as do photons of light, diffraction effects were soon discovered when electrons were scattered from crystals of nickel, or passed through thin metal foils. In theory it is possible to set up “two slit” experiments to show interference of electrons just as Young’s experiment shows interference of light. Because the de Broglie wavelength of electrons at the speeds we can handle is very much less than the wavelength of visible light it is barely possible to do these experiments in practice, but from the behaviour of electrons as revealed in other experiments there is no doubt that the results would be the same in principle as those obtained with photons, with a sinusoidal electron distribution at the screen, the density at different points on the interference pattern varying between zero and twice the average density.
6.04 Schrodinger's equation threw some light on those phenomena which seemed to demonstrate the wave nature of the particles involved, whether of light or matter, and showed how interference effects could arise when particles have two or more possible routes to a particular point on the screen. The Y values describing Schrodinger's waves were expressed as complex numbers, which can differ not only in magnitude but also in argument or phase. When added together such numbers can cancel each other because of their differing phases even when their separate magnitudes are not zero, so explaining the occurrence of the dark fringes in interference experiments. In this picture Y is a wave of probability, and the particles are still regarded as the principle actors on the stage, particles which can be detected individually in some experiments. So several questions were still unanswered. The interference pattern is produced only if both slits are open. When one slit is closed, some points on the screen receive more electrons; how do the electrons passing through the open slit “know” whether the other one is open? And when both slits are open, through which one does an individual electron pass? Or does it go through both, or neither? The Nodal theory provides an answer here, for it replies, "through neither", but a slight elaboration of the experiment seems to throw doubt on this. Suppose we shine a beam of light across the slits, so that we can observe any electrons which emerge from them. We find that electrons can indeed be seen coming through the slits, and each is found to pass through one, and only one, slit. If this were the whole story it would, of course, pose an even more impossible dilemma than the one the experiment is designed to settle, for the probability that an electron reaches a particular region of the screen D when both slits are open must equal the sum of the probabilities that it comes through the one or the other. No interference fringes could be observed, and in particular no region of D could experience less electron strikes with both slits open than with just one. But whenever we set up an experiment which would allow us to determine through which slit each electron passes, then the interference pattern vanishes. It is not difficult to understand what is happening. An electron can be seen only if it collides with at least one photon, with a random exchange of momentum and hence a change of the electron’s wavelength. The wave which passes through the other slit suffers no such change, and so the two beams lose their coherence and interference is suppressed.
6.05 But this is where a multitude of
“gee whiz” commentators took over, and did much damage to the
understanding of quantum theory during the second half of the twentieth
century. Even Richard Feynman, one of the most precise and accurate
reporters despite his lively and popular style, was tempted to
exaggerate. In the first sentence of the following quotation he almost
succumbs to the temptation, but immediately corrects himself:
If one looks at the holes or, more accurately, if one has a piece of apparatus which is capable of determining whether the electrons go through hole 1 or hole 2, then one can say that it goes either through hole 1 or hole 2. But, when one does not try to tell which way the electron goes, when there is nothing in the experiment to disturb the electrons, then one may not say that an electron goes either through hole 1 or hole 2. If one does say that, and starts to make any deductions from the statement, he will make errors in the analysis. This is the logical tightrope on which we must walk if we wish to describe nature successfully. (The Feynman Lectures III, p.1-9).
6.06 Other writers, less self-critical than Feynman, were variously attracted by the idea that a quantum system is changed
when it is observed or measured, or when “we look at it”, or “when the
results of an observation enter someone’s consciousness”. Here is one
example:
The electrons not only know whether or not both holes are open, they know whether or not we are watching them, and they adjust their behavior accordingly. There is no clearer example of the interaction of the observer with the experiment. When we try to look at the spread-out electron wave, it collapses into a definite particle, but when we are not looking it keeps its options open. (In Search of Schrodinger’s Cat, John Gribbin, p.171).
This is very misleading, and statements like this must bear some of the
responsibility for such extreme interpretations as that of John
Wheeler, who suggests that nothing in the universe really existed until
there were conscious beings capable of looking at it. He writes,
Is the very mechanism for the universe to come into being meaningless or unworkable or both unless the universe is guaranteed to produce life, consciousness and observership somewhere and for some little time in its history-to-be? (Quoted by Paul Davies, Other Worlds, p.126)
6.07 The nodal picture is much less dramatic. When interference is observed, only the wave function "passes through" the slits; the electrons do not exist there. But when we turn on the light to see the electrons as they emerge from the slits, and a photon strikes one of the electrons, then we have created a new node. The electron engages in an exchange of information there, and we know which slit it has passed through, while the momentum relayed from this node to the screen will not be the same as the original wave would have contained. The two parts of the wave are no longer fine tuned to interfere with each other, and the point where the particle strikes the screen is not constrained by the interference conditions.
6.08 To earlier experimenters and theorists it seemed that Nature was cunningly preventing us from discovering through which slit a particle passes whenever that particle is contributing to an interference pattern. But is there no way in which we can outwit her? When that particle is an electron, and we try to detect its presence by shining photons of light on the slits, the resulting collisions introduce random momentum changes which destroy the coherence of the two waves at the detector screen. But suppose we reduce the intensity of the light (and increase the sensitivity of our optical equipment). If this reduction proceeds gradually, we shall indeed see interference fringes beginning to appear as the light intensity is reduced. However, this is easily explained by the fact that there are then fewer photons. Those photons involved in collisions each have the same momentum as previously, and the electrons with which they collide are affected to the same extent, so making no contribution to the interference pattern; it is those which escape collision which continue to build up this pattern, and as the light intensity is reduced the proportion of electrons which escape increases.
6.09 Another possible approach might be to increase the wavelength of the light which we shine on the slits instead of decreasing the intensity. The momentum of a photon is given by h/l, so that the magnitude of the disturbance which the electron suffers on collision is inversely proportional to the wavelength of the incident light. This is indeed confirmed in practice, and as the wavelength increases the interference fringes do begin to appear on the screen. But at the same time it becomes increasingly difficult to form a clear image from the light scattered by the electrons, which we are examining by means of optical equipment. As is well-known, no optical arrangement allows the examination of detail smaller than the wavelength of the light with which we illuminate it, so as the interference returns we lose the ability to distinguish the position of one slit from that of the other. Nature wins again. It seems that our inability to track electrons which are contributing to an interference effect is not due simply to our poor experimental technique; some fundamental law of nature appears to be involved. This law is, of course, the Heisenberg Uncertainty Principle.
6.10 Looking at the
mathematics, we see that the formation of interference fringes is
always associated with the requirement that we add together two or more
complex wave functions (or probability amplitudes), with their inherent phase components. And when interference is suppressed we find it necessary instead to add separate probabilities,
which are real numbers containing no phase information. Feynman gives
us a simple rule for determining which of these procedures we should
follow. If two possibilities lead to final states which are
fundamentally indistinguishable, then we must add Y values, and find the resulting probability by calculating |Y|2
at the end of the calculation. But if we can distinguish between the
two possibilities, we must calculate separately the probabilitity, |Y|2,
for each possibility, and add these values in the same way that we
always add probabilities for mutually exclusive events. In Feynman’s
words,
If you could, in principle, distinguish the alternative final states (even though you do not bother to do so), the total, final probability is obtained by calculating the probability for each state (not the amplitude) and then adding them together. If you cannot distinguish the final states even in principle, then the probability amplitudes must be summed before taking the absolute square to find the actual probability.
Applying this to the present case, if the photon has a wavelength much smaller than the distance between the two slits, so that by examining the scattered light with a microscope we could decide which slit the electron has passed through, then we treat the two possible routes of the electron as real events, and add the probabilities. The distribution of electrons at the screen D then shows no interference effects. But if the photon’s wavelength is considerably larger than the slit spacing, the scattered photons do not enable us to determine sufficiently accurately where they originated, and so we add Y values for the two slits. The phase difference between the two waves as they arrive at the screen will then be significant, and interference will occur.
6.11 If we imagine the experiment being repeated many times, each time with a slightly shorter photon wavelength, we know that the interference is gradually lost, and we see that Feynman’s rule breaks down as we pass through the critical values where partial interference occurs, for in every case Feynman tells us we must either add probabilities or Yvalues. At what point are we to cease applying one formula and adopt the other? It may be thought that the Nodal interpretation suffers from the same defect. We explain the loss of coherence resulting from collisions with photons as being due to the extra node which the photons introduce into the situation; but as we gradually decrease the photons’ wavelength, and so increase their energy, at what stage do we decide that the previously non-existent node has come into being? In replying, we must remember that the only function of a node is to exchange information at a particular time and place; the question of a node’s “existence” is not important. Consider an analogy: if you ask whether a certain Mr. Smith “exists” then the answer must be just “yes” or “no”, but if you ask whether Mr. Smith has influenced your life, a yes-no answer is of little use; the answer may well be one of degree. It is possible that Mr. Smith has substantially changed the course of your life, or that he has had only small effects on it. Asking whether Mr. Smith’s influence “exists” is pointless when the real question is the magnitude (and direction) of that influence. So it is with the existence of Nodes. Whether we say that a particular node “exists” is just a matter of convenience; any significant statement concerning a node must describe the type and magnitude of its influence on neighbouring nodes. It is this influence which increases gradually as the photon wavelength is reduced, and the interference is found gradually to disappear.
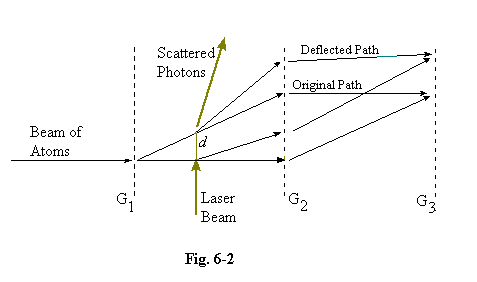
6.12 An interesting variant of this experiment was carried out in 1995 by Michael S. Chapman et.al. (Physical Review Letters, Vol.75, No.21). Chapman's experiment uses a narrow beam of sodium atoms, produced to have as small a range of velocities as possible. Instead of the single slit in screen B and the double slit in screen C it employs two diffraction gratings, G1 and G2, to split the beam and bring it together again at a screen G3, and a laser ray can be shone across the divided beam of atoms between G1 and G2. Instead of varying the wavelength of the laser, the same effect is achieved by moving the laser beam, horizontally in the diagram, in order to vary the separation of the divided atomic beam at the points where it is intersected. When the laser intersects the beam very close to G1, this corresponds to a two-slit experiment with slit separation much less than the wavelength of the photons, and interference effects should be observed at G3. Moving the laser to the right enables the effective slit separation to be changed and, as expected, the interference contrast falls to zero as the separation increases.
6.13 Another interesting
development would be possible if we could single out only those photons
which are scattered within a small range of directions, and
observe only those atoms which collided with them. These atoms would
all have had their momenta changed by approximately the same amount,
and it might be expected that, despite their collisions, they would
still display interference. Chapman and his colleagues were not able to
carry out this scheme, but they achieved the same result by observing
only atoms whose point of arrival at the G3 plane had been displaced by
a fixed amount, and did in fact find that some of the interference
contrast was retrieved. Quoting Chapman,
We have scattered single photons from interfering de Broglie waves in an atom interferometer and observed contrast loss and revivals as the separation of the interfering paths at the point of scattering is increased. Additionally, we have demonstrated that the lost coherence can be recovered by observing only atoms that are correlated with photons emitted into a limited angular range.6.14 Tony Sudbery, in describing this experiment, adds a further twist to the argument (Nature, Vol.379, p.403). He points out that, in selecting only those photons scattered in a particular direction, because of the Heisenberg relationship we have lost some of their positional information, which would have enabled us to see which of the two tracks a particular atom was following, and it is possible to regard the regained interference as a result of this ignorance. He writes,
However, the coherence is not really lost: it has been extended to involve properties of the measuring apparatus ... In the experiment of Chapman et.al., however, the apparatus could be taken to be the single photon that scatters off the atom, and the coherence in the extended system consisting of the photon and the atom is revealed in the interference patterns associated with photons moving in particular directions.
He reminds us that if we did not thus select a sub-set of photons, but instead observed a wider group, for instance by focussing them in a microscope, then we could determine which path each particular atom had followed, and there would be no interference. But because the microscope requires a large angular aperture, we would at the same time loose accurate information concerning the photons' directions. He then goes on,
A slight extension of the experiment pushes one uncomfortably close to paradox. In principle one could delay the observation of the photons, and the decision whether to focus them or measure their direction, until after the atoms had formed their pattern.The Nodal theory can agree with all this, except that the result need not be described as paradoxical, with the implication that our decision to observe only those atoms associated with a subset of photons in some way changes the past. The distribution of atoms at screen G3, corresponding to any restricted selection of photons, forms a pattern of light and dark bands. But the position of the pattern will differ for different selections, and if all groups are combined, the overlapping patterns show no such bands. It is unhelpful to regard such a fact as paradoxical.
6.15 The interpretation of interference effects can often be accomplished most easily by considering the transfer of information. We have shown that an atom is prevented from contributing to interference if a colliding photon takes away sufficient momentum to destroy the coherence. Indeed, careful consideration of the possible transfer of momentum which can occur will often provide an accurate indication of the degree to which interference effects will be observed. Now momentum is a part of the information carried by the wave function of a particle. Its wavelength is directly related to that momentum, so it is not surprising that tracing the way this information is distributed after a collision or a series of collisions will tell us much about potential interference effects.
6.16 The Nodal interpetation takes this argument further. Between one node and the next the wave contains the only record of the particle's momentum. And we claim that the nodes consist only of the tranferrence of information which occurs there. We are deliberately ambivalent about the degree of "reality" we ascribe to the NWF, but there can be no doubt about the reality of the information. Perhaps the universe consists only of information.
6.17 Nodal theory provides its own replies to each of the other problems which interference phenomena present. The answer it provides to the duality question, whether electrons and photons and other particles consist of waves, or particles, or both, or neither, differs substantially from the explanations offered by other theories. The particles themselves do not exist, but the points where they collide do. As every theory must agree that the particles cannot influence our senses or measuring apparatus except at points of collision, the observations we make of any system must inevitably be exactly the same as if the particles did follow continuous trajectories, so it is not surprising that all previous theories have supposed their existence to be real. The information linking one node to another also exists, and the NWF is our picture of the channel through which it is transferred. Our own prejudiced position, knowing about the past but not the future, complicates the probability role of the waveform, but if we separate out the elements which are subjective, the information which remains must continue to involve an element of probability, which we investigate in Chapter 11. We know that, given the positions of all the past nodes of a system, there is not sufficient information to determine uniquely the positions of future nodes, but some positions are more likely than others, and this reflects the probability element in the linkage. Notice that exactly the same would be true if we regarded time to flow in the opposite direction. Given the positions of all future nodes of a system, there would not be sufficient information to determine uniquely the positions of past nodes, and a different set of probabilities would be involved.
6.18 When we are asked which slit the photons pass through in Young's experiment we answer "neither". But the wave has access to the whole of space-time, and so it "knows" whether or not both slits are open. It is useful to picture the wave as passing through the two slits, although we must remember that this may be no more than a picture. The wave consists only of information; provided the necessary information is available at each node it does not matter how it gets there. The railway timetable giving information about trains from London to Edinburgh does not need to make the journey itself.
6.19 So the loss of interference in particle experiments, when attempts are made to determine the paths of individual particles by illuminating them with a beam of photons, is explained in the nodal theory in terms of information loss. A complete understanding is provided if we consider the transfer of momentum, remembering that momentum is not to be thought of as a property of moving, massive particles, but as a component of the information linking adjacent nodes to each other. Bearing this in mind, together with the fact that some recent experiments have involved a subtle selection of particles to produce interference, or to restore interference effects which had been supressed, should remove the element of paradox which some researchers have suspected.
(c) Hector C. Parr (2002)
Previous Next Home Hector Parr's Home Page