Ch. 1
Ch. 2
Ch. 3
Ch. 4
Ch. 5
Ch. 6
Ch. 7
Ch. 8
Ch. 9
Ch.10
Ch.11
Ch.12
App.1
App.2
App.3
Biblio.
Index
Hector Parr's Home Page
Quantum Physics: The Nodal Theory
Hector C. Parr
Chapter 2: Time
2.02 It seems to us that we live in a three-dimensional world of space, and that the material world which exists in this space changes from moment to moment as time advances. But surprisingly, all the mathematical equations and relationships which describe this world contain nothing corresponding to the idea of change. The basic units with which the fundamental sciences deal are not things in space, but events in space-time. The equations describing the motion of bodies, whether in everyday life, in atomic phenomena, or in behaviour on the large scale requiring the techniques of relativity theory, all involve the variable t as well as x, y and z, and these four variables occur on equal terms. They describe, in fact, a four-dimensional world, and one which is essentially static. The idea of change is not represented in this description by anything moving or altering, but simply by the different patterns of events which are found corresponding to different values of the t co-ordinate, just as events at different places are represented by points with different values of x, y or z.
2.03 We are unable to visualise four dimensions, but for purposes of illustration we can often dispense with one of the space dimensions, and the z co-ordinate can be omitted. We may then represent events on a perspective drawing with the x and y axes in the horizontal plane and the t axis drawn vertically upwards. The life-history of a small body or a particle of matter is represented by a line which we call its "world-line", showing its continued existence throughout a period of time, and its movement is represented by the slope of this line, the angle it makes with the t-axis.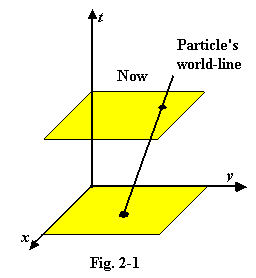
The state of the world at the particular time we call “now” or the “present” is represented by everything on a horizontal plane drawn for a particular value of t. And we can imagine the progress of time being represented by this plane moving slowly upwards at constant speed. The strange fact that our mathematical descriptions of the world contain nothing corresponding either to the “now” plane, or to its upward movement, need not imply that our impressions are wrong; perhaps the mathematical descriptions are just incomplete.
2.04 This picture might be thought
of as no more than an interesting way of representing the relationships
between events, while not really indicating anything about the world
itself. But this view had to be abandoned at the beginning of the
twentieth century with the acceptance of Einstein’s Special Relativity
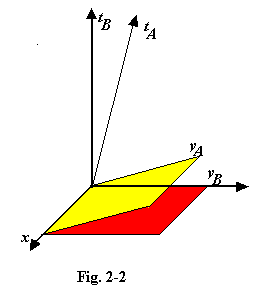
theory. The x, y, z, t picture was suddenly seen to present a
much closer view of reality when Einstein showed that, just as the
choice of directions for the x, y and z axes is arbitrary, so too is the direction of the t axis and the plane we adopt for our x-y
co-ordinates. Einstein shows that both of these are dependent upon
one’s state of motion. If an observer A is moving relative to B, then
A’s x-y plane must be inclined to B’s by an angle which can be
calculated easily from Special Relativity theory. This shows that we
must abandon the belief that the “now” plane is universal, that my
"now" plane is necessarily the same as yours. Expressing this
differently, Einstein has shown that the notion of “simultaneity” is
meaningless. Relativity reveals many simple situations in which two
events which one observer describes as simultaneous, to another
observer are separated by a measurable time interval. We discuss this
more fully in Chapter 10. At any particular point in his life, an
observer is still free to imagine his own “now” plane if he wishes, but
it is purely personal, and has no existence outside his own
imagination. And if the “now” plane has no intrinsic existence in the
outside world, neither can the motion of a universal “now” plane be
real. The idea of a moving time is false; it exists only in the minds
of individuals.
2.05 Indeed it did not require Einstein to show that the notion of a “flowing” time is a nonsense. If the time is continually flowing or changing, as our natural intuition suggests, with respect to what does it change? One thing can change only with respect to another. Usually when we talk about change we mean change with respect to time itself. The rate at which a vehicle changes its position is its speed, measured perhaps in miles per hour. The rate at which an investment earns interest is measured as a percentage per annum. Mathematicians represent the rate of change of any quantity x by the symbol dx/dt. But time cannot be said to change with respect to itself; dt/dt is meaningless.
2.06 There is an even more challenging deduction from this line of thought. Not only do we think of our “now” plane as steadily advancing as we go through life, but at any moment of time it appears to divide the history of the world into two very different regions. All the events below it have happened. There is nothing we, or any one else, can do to alter them. But all the events above it lie in the future. Even if we can try to predict some of them, they seem to lack the degree of certainty possessed by events which lie in the past. Indeed we like to think that we ourselves can be responsible for them. We believe today’s decisions and actions help to “shape the future”, but it never occurs to us that we can change the past. And yet the arguments presented in this chapter show that we must now dismiss these impressions as illusory. If there is no universal “now” plane to separate the certain past from the uncertain future, there can be no intrinsic difference between events which lie in the one region from those which lie in the other. All events in the world’s history, past present and future, must be equally certain and unalterable.
2.07 Another important element in our impressions regarding the nature of time is manifest in our intuition concerning the irreversibility of many processes we observe. We are amused when shown in reverse a moving picture of someone shuffling a new pack of cards, an egg being broken into a dish, a river flowing downhill, or an electric fire cooling down when switched off. We know that cards do not sort themselves into numerical order, broken eggs do not transform themselves into whole eggs, and electric heaters do not spontaneously heat themselves when disconnected from their power source, but we seldom consider why this should be. Some of the formal consequences of this irreversibility are seen in the science of Thermodynamics. The Second Law of Thermodynamics can be expressed in many different ways, but perhaps the simplest is to say that heat always flows from a hotter body to a cooler, and never the reverse. We know that, when we turn off a fire, the heating element cools until it has reached the same temperature as its surroundings, but it then remains constant. The laws of thermodynamics were gradually formulated during the nineteenth century as engineers strove to improve the efficiency of the newly developed steam engine. They came to realise that heat is just one form of energy, of which every body contains a certain amount, but that this energy cannot be transformed into a useful form unless temperature differences exist between different parts of an engine, for instance the furnace and the condenser of a steam locomotive. They devised the concept of entropy to describe the usefulness of the energy in a system. Thus, after an electric fire has been turned off, the total heat energy in the fire and its surroundings remains constant as the element cools, and its surroundings are warmed slightly, but the entropy gradually increases as the two temperatures approach each other. The Second Law of Thermodynamics tells us that the entropy of any closed system cannot decrease, and usually increases, as time advances. As the science of Thermodynamics developed, the notion of entropy helped in the description of processes involving heat transference and the working of steam engines, but it was subsequently found to be applicable to a wide range of other phenomena. Of special importance to us in our investigation of the nature of Time, as we shall see, is the application of entropy to a system of bodies moving under the influence of gravitational forces, and to the universe as a whole.
2.08 The very familiarity of processes which are essentially irreversible makes their explanation more difficult. Indeed it has only gradually come to be realised that any explanation is required, and many who have attempted to understand them have been led astray by subtly assuming that which they are attempting to prove. The difficulty of the problem was only slightly lessened when it was realised that all manifestations of the Second Law have one thing in common, namely that the later state of a system is almost always a more probable state than the earlier state. It is more likely that a pack of cards are in random order than that they are sorted, for there are many more random orderings than sorted ones; if the molecules of an egg lie in a basin, it is more probable that the yoke and white will be mixed together than completely separate; and if we know the average energy of all the molecules of the gas contained in a flask, it is more probable that the energies are distributed randomly than that the molecules in the left half have a greater average energy than those in the right. But in attempting to explain why the more likely situation always seems to occur at the later time, we are very prone to be led astray because the fact seems so obvious. And we are likely also to overlook the most paradoxical element of this question. All the fundamental laws of physics, including the laws of mechanics which describe the motions of the molecules of a gas, and which explain their behaviour not only as they move unimpeded between one collision and the next, but also as they collide with each other and with the walls of the containing vessel, these laws are all time symmetric. If we represent the motions of a small number of molecules as a moving picture and view this with time reversed, the molecules will continue to obey the same laws. We would be unable, by viewing such a moving picture, to determine whether it was being displayed correctly or in reversed time. The mystery which requires explanation is how the time-symmetric laws which govern the motion of the individual molecules can give rise to the time-asymmetric Second Law which describes, on a less detailed scale, these same motions.
2.09 The great nineteenth century physicist Ludwig Boltzmann (1844-1906) attempted to answer this question with his so-called H-Theorem. He knew that, when the molecules of a gas in a container were in a condition of equilibrium, corresponding to what we would today describe as maximum entropy, the statistical distribution of energies of the individual molecules took a particular form which had been derived by Clerk Maxwell (1831-1879) several years previously. Boltzmann presented a proof of the fact that any other distribution of velocities would steadily change until the equilibrium state was reached. If, for instance, the molecules in one half of a container have a higher average energy than those in the other half, this state of affairs will dissipate as time progresses and the high energy molecules collide with those of lower energy. His proof was viewed with suspicion by several physicists of the day, and a number of challenges were mounted. These all hinged upon the fact that possible states of motion could be postulated which would result in a decrease rather than an increase of entropy, and a movement away from equilibrium. Imagine, for example, a gas which was formerly in an unstable state, perhaps with a temperature gradient across it, but which has now reached equilibrium. If we suppose that each molecule has its velocity reversed the gas will then trace in reverse its previous history, and entropy will steadily decrease. It is irrelevant that we know of no way to bring about this reversal; the reversed motion is perfectly possible, and in fact is as likely to occur by chance as was the actual motion before reversal. Arguments of this sort show that Boltzmann’s proof of the H-Theorem must contain a flaw, and as a result Boltzmann came to realise that what he had proved was not a certainty but rather a situation which was overwhelmingly likely to occur. The fact that, in this new form, the H-Theorem still did not explain how a gas evolved in a time-asymmetrical manner as a result of the time-symmetrical behaviour of its molecules, was still not fully realised by either Boltzmann or his critics, and led to almost a century of argument, much of which was of no consequence because the protagonists were themselves misled by their deep-rooted misconceptions of the irreversibility of time itself.
2.10 Only gradually was it realised that the Second Law did not result from the fundamental laws of science, for these are time-symmetric, and nor did it arise because of any statistical asymmetries. In fact it is a purely empirical fact, arising from the very special state of the matter in the universe at the present time. What requires explanation is not the movement of the universe towards higher entropy, towards an increasingly probable or disordered state; rather it is why entropy today is so low, and why the universe is at present in such an unlikely state. Almost everything of interest that happens on earth, including the sorting of cards into numerical order by humans, the manufacture of eggs by hens, and the raising of water vapour to the tops of mountain so that rivers can flow downhill, is ultimately a result of the large temperature difference which exists between the earth and the sun, a manifestation of low entropy to which we, and all living things, owe their existence. The problem thus becomes one for cosmologists rather than heat engineers, and in recent years they have begun to make some progress in solving it. They are revealing that the unsolved question is one of gravitation rather than of heat. The sun and the stars shine only because they have condensed by gravitational attraction from more tenuous and more homogeneous matter, and the question for the cosmologists is why this did not happen long ago, resulting in all the matter in the universe condensing into one enormous mass or one black hole. They are showing us that the expansion of the universe is an essential part of the explanation, for it clearly acts in the opposite direction to gravitational attraction. But they also tell us that the degree of homogeneity of the early universe must have been critically determined for it to have persisted for so many billions of years, and yet still not have reached equilibrium, with all its matter condensed into one mass, or at least with everything at the same temperature. If the early universe had been slightly too uniform it would not yet have condensed into galaxies and stars, while if it were insufficiently uniform the condensation would have proceeded too far, with the galaxies already collapsing into black holes. Everything depends on the nature of the big bang, which is far from being understood at the present time. For our purposes it is not necessary to pursue this further; it is sufficient if we acknowledge that the conditions soon after the big bang were such that entropy has remained far below its maximum value for some fifteen billion years, and we are witnessing the universe during an era when its gradual “running down” is producing some fascinating phenonema, including ourselves!
2.11 In the previous paragraph we talk about movement, things happening, the universe expanding and the stars condensing. Is not this all in the language of a flowing
time, a concept which we have just described as “nonsense”? It is,
indeed, but we often need to use such language because we have no
other. Our language evolved long before anyone questioned whether time
flowed and things happened, or before anyone thought of picturing the
four dimensions of space-time. But we can often clarify our thinking by
translating such language into the more accurate descriptions provided
by pictures of the corresponding static structures in space-time. Let
us apply this technique to a consideration of the expansion of the
early universe. In our picture we must represent time by the
distance from the centre of our diagram rather than by distance up the
page, and we can then represent the whole of space at any particular
time by a circle whose radius corresponds to that particular time. We
thus get a very simple picture in two dimensions only, with the three
dimensions of space portrayed by the one dimension of the circumference
of a circle. The resulting pattern resembles the lines of latitude and
longitude around the North Pole, with time represented by the meridians
and the whole of space at any particular time represented by one of the
circles of latitude.
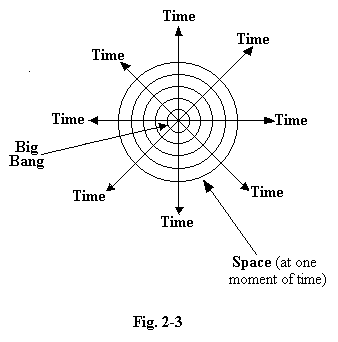
The world lines of particles of matter and radiation then become lines radiating from the pole, always extending in a generally outward direction, but deviating slightly from the lines of longitude to show their intrinsic motion, and meeting each other where our picture needs to represent their collisions. The homogeneity of the early universe, which was so finely tuned to give us the sort of world we now find, is represented on our picture by “boundary conditions” which these world lines must satisfy close to our “North Pole”. A familiar and useful analogy is provided by the electric field around a small charged body; the distribution of charge on its surface provides the boundary conditions which determine the electric field close to the surface, and this in turn determines uniquely the direction and strength of field throughout the whole space influenced by the charged body. In the same way, the whole future of the universe is constrained by the boundary conditions at the big bang. That future is not uniquely determined because of various types of uncertainty which we shall discuss later, but the general macroscopic picture is dominated by the very low entropy represented by the homogeneity of the world-line distribution near the pole, and the Second Law is our description of the increasing entropy at greater distances (i.e. later times), and particularly by the clumping together of world-lines under the influence of gravity.
2.12 We must examine some further consequences of the Second Law. We have seen that the law does not apply to micro-systems consisting perhaps of a small number of molecules, or the collisions of a small number of atomic or nuclear particles, for reactions of this type are always time-symmetric; if they had a degree of asymmetry in the very early universe they have long ago worked this out of their system. The Second Law does apply to macro-systems such as packs of cards, eggs, and flasks full of gas, where we are not interested in the behaviour of individual molecules, but only in larger scale characteristics such as temperature or pressure. It was pointed out that the Second Law can be pictured informally as a progression to states of increasing probability, i.e. towards macro-states which would arise from increasing numbers of possible micro-states. Another useful picture is presented when we realise that processes which proceed to higher values of entropy always contain some element of dissipation, or dispersion. A new pack of cards is arranged in perfect order, and as shuffling progresses this order is gradually dispersed through the pack; at first there will still be groups of cards which are in numerical order, but these groups become smaller, and more numerous, until they are completely dissipated throughout the pack. When a hot body cools to the temperature of its surroundings, its heat energy is gradually dissipated throughout a greater volume of matter. And almost all the processes we see around us are dissipative in some way. Those that seem to go against this rule, such as heat engines, refrigerators, or the evolution of life itself, will all be found on examination to involve a greater degree of dissipation into their environment, a greater overall increase in entropy, than the decrease which they themselves represent. Entropy always increases in any self-contained system. The answer to the question of why some parts of the universe are still far from equilibrium is that the organisation they display is left over, as it were, from the highly ordered state of the early universe. They are still linked to the boundary conditions existing just after the big bang.
2.13 An important example of the irreversible dissipation of such structures is shown whenever a system generates a record of itself, whereby a picture or copy is made of some of its characteristics, for elements of the structure of this system are duplicated in the record. This is dissipation, albeit in a minimal form; whereas there was formerly just one instance of these elements there are now two or more. Regarding the process of record-making in this way, it is seen how the Second Law provides a simple explanation of the fact that records can exist only of past events. Consider, for example, the making of a number of copies of a document in a photo-copier. The original and all the copies contain no more information than the original itself, but this information is distributed more widely after the copies have been made, which is thus an irreversible process.
2.14 A most significant example of record formation exists in the human brain, the laying down of memories. As we shall see in later chapters, the existence of memories of past events, and the impossibility of having memories of the future, plays a large part in the muddle which has characterised attempts throughout the twentieth century to understand quantum behaviour. So long as we believe that the asymmetry of record formation and memory formation is just obvious, and requires no explanation, just so long will the muddle remain unresolved.
2.15 Thus we see that our common perception of the nature of Time carries with it four features which are false, and which are prone to mislead us in our thinking about the real world:
(i) We believe that the particular moment of time which we call “now” (and which we will denote by t0) has an objective significance independent of our own minds, and that the whole universe shares this same value of t0.
(ii) The value of t0 seems constantly to increase at a constant rate (whatever that may mean).
(iii) The time t0 appears to divide the history of the universe into two parts, events occurring at times t for which t < t0 appearing to have a degree of certainty not enjoyed by those for which t > t0.
(iv) We accept the Second Law of Thermodynamics believing it to require
no justification. In other words it seems natural that entropy should
increase, and that systems become more disordered as the value of t increases, and never the reverse.
2.16 In the remainder of this chapter we shall try to determine why we have these false impressions, and what we can do to prevent them from leading us astray in our attempts to understand the fundamental workings of the universe, and in particular the interpretation of quantum phenomena.
2.17 Our belief in an objective and universal “now” is not difficult to understand. Every event has a position in space and a position in time. And every thought we have is an event; it is situated in our brain, and it occurs at some particular point in time. At the same moment that we experience a thought there are usually other events going on around us, and it is natural to suppose that more remote events of which we are not aware, even events at the other end of the universe, will be occurring at this same time. This present moment has a special significance for us. It is the time when things happen to us, and the moment at which we are acting; indeed it seems to us to be the last possible instant at which we can affect events lying in that moment’s future. So it is natural for us to suppose that this particular t value is special in its own right, the time at which everyone else is being affected or is making decisions, the moment which has been reached by the whole universe.
2.18 More difficult to explain is the overriding impression we have that this “now” is constantly advancing, that time constantly changes or flows. This sensation is certainly related to our possession of memory; if we had no memory, not even of the events which immediately preceded the present moment, we could have no feeling of the progression of time. It is the memories we have of our past life that make plausible our belief that we have lived that life up to the present moment, re-inforced by all the external records we have of that past life, and we hope and believe we shall continue living it in the future, collecting more records and memories along the way. But suppose, for a moment, that some process we do not understand could build up in a person’s mind all the memories relating to a life which that person had not lived, and could back up these memories with physical records, or at least with the impression of the existence of these physical records relating to that fictitious life. There is no way by which the person could detect the deception. He or she would believe that life to have been real, and would be led thereby to believe that throughout life, time had been passing, just as we do. We see that, through the agency of memory and record keeping, our belief in a flowing time can be explained, despite the fact that, as we have shown, such a conception is meaningless or nonsensical.
2.19 The possession of memory can explain also our belief in a fundamental difference between the past and the future. We know that past events have occurred because we can remember them, or because we have records of them. And if we have doubts we can often confirm our knowledge by comparing our memories or records with other people’s. When allowance is made for human fallibility, the agreement between different people’s recollections of events which they observed in the past is remarkable, and very difficult to explain if these events did not happen. Because some of these memories and records persist over long periods, it is clear that past events cannot be changed, for this would make false our memories of them. But the future, we believe, is another matter. We may sometimes make predictions, but this can be done only by surmise and calculation; predictions of future events do not have the same degree of certainty as memories of past ones. Indeed, we believe that people are sometimes able to affect future events in a way that they cannot influence the past. (The issue of free will is much too complex and controversial to discuss here; but many philosophers are now in agreement that the term “free will” becomes increasingly vacuous the closer one seems to a rational definition). So it is not surprising that we attribute the uncertainty of future events to the events themselves rather than to the limitations of our own faculty of memory, even though we now acknowledge that the past and the future cannot differ fundamentally in this way because the dividing moment which separates them, the “present” moment, has no objective existence.
2.20 We have discussed the Second Law of Thermodynamics, the (almost) universal tendency for systems to become increasingly uniform in temperature, to be in a state of greater probability, to present a greater degree of dissipation, as the value of t increases. Because this affects everything we experience, everything we think, everything we do, it is not surprising it becomes so familiar in the earliest days of our childhood that we accept it unthinkingly just as one of the laws of nature, like the effects of gravity, the impenetrability of solid bodies, or the heating effects of fire. We cannot be expected to know in these early days of our life that the fundamental laws of physics are in fact time symmetric, and that the asymmetry of most macroscopic phenomena is just an empirical fact pertaining in the particular universe we happen to inhabit. If great physicists such as Boltzmann could believe mistakenly that future events are dependent on past ones in an irreversible relationship, we need not be ashamed if we occasionally fall into the same trap. But we must try to minimise the number of such mistakes by constant vigilance.
2.21 Whenever we are in danger
of being led astray by an unconscious belief that our own personal
“now” actually has some objective or external existence, or that the
space-time picture of the universe “changes” as time flows or
progresses, there is a simple remedy. We should draw, or imagine, a
representation of the four dimensional picture of the events we are
considering, and firmly resist the temptation to draw on it the plane
representing our “now”, and even more firmly refuse to imagine such a
plane moving along the time axis. As a simple illustration, the diagram
represents a collision between two balls on a billiard table. Such a
table is conveniently two-dimensional, so we do not need to discard a
dimension in our representation. The illustration is static; the movement of the balls is completely represented by the slope of their world lines.
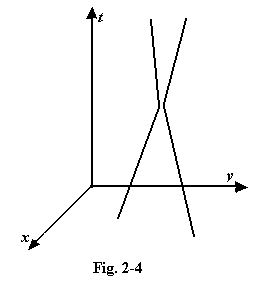
2.22 The tendency to imagine things moving on a space-time diagram is more persuasive than may be imagined, and has led some capable thinkers into error. One sometimes reads about the possibility of things moving “backwards in time”, and an author may illustrate the idea with a space-time diagram like that shown here. We are asked to believe that the line from A to B represents a particle moving forwards in time between two points, whereas if the movement on the diagram were from B to A, it would represent a particle moving in reversed time.
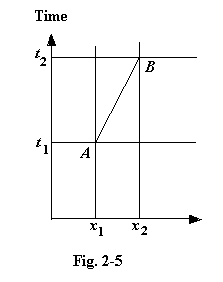
But what is the difference between the behaviour of these two particles? The first is at x1 at time t1 and at x2 at time t2; the second is at x2 at time t2 and at x1 at time t1. So they are both at A at the same moment and both are at B at the same moment. They travel together from the point A to the point B, and may indeed be the same particle. This is clearly not how the authors expect us to think about it, for they had tried to distinguish a particle "moving" from A to B from one "moving" from B to A. We must always remember that the space-time diagram is static; it will serve its purpose of banishing our temporal illusions only if we firmly disallow any view of it which involves movement.
2.23 Much less rational is a lot of the
literature relating to time travel into the past. Many a physicist or
philosopher has been kept awake at night worrying about the “closed
causal chains” which we shall be able to create when we master the art
of time travel. The favourite story is of the man who journeys back to
a time before his parents were born and murders his grandmother.
Because of this, he could not have been born, so he couldn’t have
murdered his grandmother, and so he would have been born .... Critics
point out that such a closed chain can not exist, since relativity
teaches us that nothing can move faster than light. The world-line of
any material body must always lie in a generally "time-like" direction
on the space-time diagram, and with a suitable choice of scale no
world-line can make an angle of more than 45o with the time
axis. It is therefore impossible for it to double back on itself, and
closed loops are impossible. But then topologists invent space-time
topologies, such as cylinders or “worm-holes”, wherein such closed
loops could exist, and the heart-searching begins again. But
what is the problem? If we look at the situation as laid out on a
space-time diagram, with nothing allowed to change, even believers in
time-travel must admit that the unfortunate grandmother either was
murdered or she wasn’t. If she was, her grandson never exists and the
murder was committed by someone else.
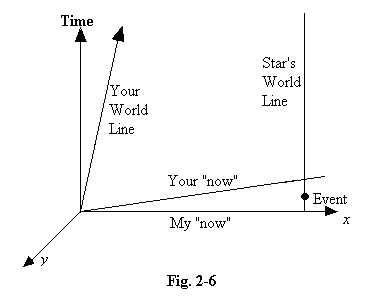
2.24 A similar space-time diagram can be used to illustrate the distance- and time-transformations of Special Relativity, and this can drive home the point that the future and the past cannot differ in certainty in the way our intuition suggests. Suppose that I am standing on the platform at York while you pass on the London to Edinburgh express, and suppose that a large meteorite crashes onto a typical star 800 light years away. The diagram shows how our two “now” planes would be related, and shows it to be quite possible that the event occurred half an hour ago relative to your “now”, but will not occur for another half hour for me. Does the event lie in the immutable past or in the uncertain future? It is clear that no such distinction can exist.
2.25 As we have seen, some systems and some processes are time-reversible and some are not. It is important for us to understand what sorts of process are of the one type, and which sorts are of the other, and here there is another powerful mental image we can call upon to help us in our task. We can imagine a process to be recorded in a video camera and played back in reverse; then if it is truly symmetric the reversed sequence of frames will still appear plausible. In fact we should not be able to distinguish the forwards from the reversed sequences, unless we know by some other means which actually occurred.
2.26 Suppose we have a pair of idealised billiard balls which are totally smooth and elastic, so that when they collide on a billiard table there is no loss of kinetic energy. Given the speed and direction with which each is travelling, and the orientation of the line of centres at the moment of collision, it is easy to calculate their speeds and directions after collision. And if we then imagine that these final velocities are reversed to produce another collision, the resulting speeds will be the reverse of what fomerly were the initial speeds. Being shown a video recording of such a collision, we would be unable to say whether it was being played correctly or in reversed time. But now suppose that one of these balls is replaced by a lump of clay, which does not fully recover its original shape after a collision; will the collision still be reversible? To find out, let us imagine the video is shown to us in reverse. A deformed lump of clay, bearing the imprint of the solid billiard ball, collides with such a ball, whereupon the imprint is removed and the clay becomes a perfect sphere. We see at once that this is impossible; the imprint is a result of the collision, and so must be present afterwards, not beforehand. This sort of process is so familiar that we assume it to be universal without giving it a second thought. If your leg is in collision with the table leg, it will be bruised after the collision, not before; the collision could not remove a bruise which was there beforehand. When we copy a picture in a photocopier, the new image is on the paper after it has been copied; the photocopier does not remove an image which was there beforehand.
2.27 And in this familiarity lies the danger. This was the error made by Boltzmann in his fallacious proof that the collisions of molecules in a gas must result in an increase of entropy, in other words must result in the energies of the molecules becoming more uniform rather than less. He made the assumption, which must have seemed very reasonable to him, as it still does to us, that the motion of a pair of molecules after they have collided is influenced by the fact that the collision did occur; their motions before the collision are not influenced by the fact that they will collide in the future. But view this assumption in reversed time and we see immediately that it introduces an asymmetry which is known not to be present; molecules are known to behave just like perfectly elastic billiard balls when they collide. We are more familiar with lumps of clay, bruised legs and photocopiers than we are with molecules of a gas, and we must ask why these latter behave so differently and counterintuitively. The essential difference is that lumps of clay are composite bodies; they have structure, and this structure is modified by a collision. Not only does the surface bear an imprint afterwards, but its molecules are set in motion which continues, resulting in a slight rise in temperature. Here is another example of what we have called “dissipation”, and herein lies the time asymmetry, for the random motion of the clay molecules by virtue of their higher tempertaure is a more probable state of affairs than the equal velocities which they all possessed by virtue of the previous motion of the clay. And a lump of clay is more likely to be in a deformed state than to possess the form of a perfect sphere.
2.28 As we study the strange world of the quantum, we must frequently view processes as static models in the four dimensions of space-time. And we must ask ourselves how the explanations we formulate would appear in reversed time, to prevent ourselves being misled by the deeply ingrained false impressions our intuition gives of the nature of time.
(c) Hector C. Parr (2002)
Previous Next Home Hector Parr's Home Page