Ch. 1
Ch. 2
Ch. 3
Ch. 4
Ch. 5
Ch. 6
Ch. 7
Ch. 8
Ch. 9
Ch.10
Ch.11
Ch.12
App.1
App.2
App.3
Biblio.
Index
Hector Parr's Home Page
Quantum Physics: The Nodal Theory
Hector C. Parr
Chapter 9: The EPR Problem
9.02 The authors of the original EPR
paper described a thought-experiment in which an elementary particle is
made to split into two equal parts, which than fly apart. Because of
the law of momentum conservation, the two parts must travel with equal
and opposite velocities. Now the complementarity laws of Bohr’s quantum
theory decree that if we know accurately the position of a particle we
cannot at the same time know its momentum. Furthermore, Bohr maintained
that this lack of precision was not the result of clumsy measurement;
we can talk about the momentum of a particle only in relation to a
particular arrangement of measuring apparatus, which could not exist
alongside apparatus for measuring the position of the particle at the
same time. Bohr seems to say that the momentum has no real existence except in relation to the apparatus used to measure it. But the EPR paper pointed out that if we measure the momentum of one of the pair of particles we immediately know the momentum of the other,
and the authors maintained that this shows the latter momentum to have
a real existence, whether or not it is measured. They wrote:
If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity. ... [It follows that] quantum mechanics does not provide a complete description of physical reality.
Bohr defended the opposite point view with arguments such as the following:
The apparent contradiction in fact discloses only an inadequacy of the customary viewpoint of natural philosophy for a rational account of physical phenomena of the type with which we are concerned in quantum mechanics. Indeed the finite interaction between object and measuring agencies, conditioned by the very existence of the quantum of action, entails ... the necessity of a final renunciation of the classical ideal of causality, and a radical revision of our attitude towards the problem of physical reality. ... From our point of view we now see that the wording of the above-mentioned criterion of physical reality proposed by Einstein, Podolsky and Rosen contains an ambiguity as regards the meaning of the expression ‘without in any way disturbing a system’. Of course there is in a case like that just considered no question of a mechanical disturbance of the system under investigation during the last critical stage of the measuring procedure. But even at this stage there is essentially the question of an influence on the very conditions which define the possible types of predictions regarding the future behaviour of the system. Since these conditions constitute an inherent element of the description of any phenomenon to which the term ‘physical reality’ can be properly attached, we see that the argumentation of the mentioned authors does not justify their conclusion that quantum-mechanical description is essentially incomplete.The two men continued to discuss their differences for several years, and had come no closer to agreement at the time of Einstein’s death in 1955.
9.03 The actual thought-experiment described in the EPR paper was never actually performed. But in 1951 David Bohm shifted the discussion sideways by suggesting an alternative experiment which might be easier to perform in practice, and which also widened considerably the philosophical challenges which it posed. It is experiments of the type Bohm invented which have subsequently come to be accepted as the authoritative version. The pair of identical particles which these experiments envisage are to be either protons, whose spins must be oppositely directed in order to conserve angular momentum, or photons which, if linearly polarised, must share the same axis of polarisation. The measurements which are to be performed on the two particles are measurements of spin, which in the case of photons are easily carried out by attempting to pass them through polarising filters. If a photon is transmitted by such a filter, conventional quantum theory maintains that its axis must then become oriented with that of the filter, whereupon conservation laws decree that the other particle of the pair must at the same moment be affected in the same way, however remote it is. Two conclusions follow immediately. If the two filters have their axes parallel to each other, then whenever one photon is transmitted by the filter it encounters, the other photon must be transmitted also, and whenever a photon is stopped by its filter, then so must the other. If, alternatively, the filters are set up with their axes perpendicular to each other, then one photon of the pair must always be transmitted, and the other absorbed.
9.04 There
seemed little doubt that this effect would be observed if the
experiment could actually be performed, and many writers then assumed
this would show the two particles were communicating with each other in
some way after they have separated, or were somehow “aware” of the
setting of the polarisers before they encountered them, for how
otherwise could they display the degree of co-operation observed? Many
books written by physicists and mathematicians during the last thirty
years describe this effect, and several of their authors declare,
erroneously as we shall show, that the results prove the existence of
such non-local influences. The EPR effect does present us with
some strange contradictions, but they are not displayed in the simple
case we described above, where the two polarisers have their axes
parallel or perpendicular. Paul Davies, dealing with the case in which
the axes of the two polarising filters are parallel, writes:
The truly mind-boggling implications of [the experiment] are apparent if we use two parallely orientated polarizers, one of which is stationed in the path of each of the two correlated photons. Because the polarizations are forced to be parallel, whatever we measure for the photon polarization of one we are obliged to find the same for the other, but as there are only really two polarization states that are measurable (i.e. parallel and perpendicular) the 'yes-no' decision of one polarizer must be identical to that of the other. ... The mystery is, how does the second polariser know that the first one has let a photon pass, so that it too may do the same? The experiments could be carried out simultaneously, in which case we can be sure, on the basis of the theory of relativity, that no message can travel faster than the photons themselves between the polarizers to say 'let this one pass'. In fact by stationing the polarizers at different distances from the decaying atom we could arrange for either experiment to be performed before the other, thereby ruling out any question of one polarizer signalling the other, or causing it to accept or reject a photon. (Other Worlds, Penguin, 1980)
9.05 There
is no need for Davies' astonishment. We may agree that information
could not be transmitted from one photon to the other fast enough to
ensure their cooperation, but the two photons themselves can
carry information, and may well have “agreed” a common policy before
they separated. We will show a simple method which photons could employ
to meet these requirements without having to pass any information to
each other after the moment when they separate. Suppose their (common)
spin axis is chosen randomly within the range 0o to 180o, and that a photon always passes through a polariser if its spin axis makes an angle of less than 45o with the optical axis of the polariser, and is always stopped by the polariser otherwise.
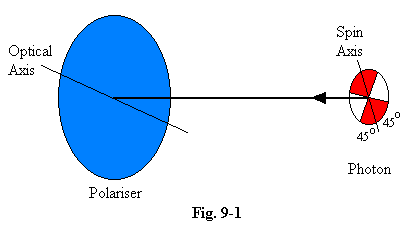
In the diagram, we are supposing that a photon is transmitted by a polariser whenever the axis of the polariser lies within the red sectors, but is absorbed if the axis lies in the white sectors. It is easy to see that, whenever a random photon meets a polariser, the probability of transmission is 50%, as it should be, and in the experiment we are considering, with the optical axes of the two polarisers parallel, the two photons are always either both transmitted or both absorbed. It is equally easy to see that, in the alternative case where the polariser axes are perpendicular to each other, one photon must be transmitted and the other is not. We are not suggesting that this is indeed the explanation of how the EPR results are obtained, but the picture does show that the results quoted by Davies are not as remarkable as he imagines. The true EPR paradox is much more subtle.
9.06 So far we have considered only cases in which the two polarising filters have their axes parallel or perpendicular. If the angle between the axes has any other value, say qo, then quantum theory predicts, and no-one doubts, that the results of our experiment would be as follows: the probability that both photons are transmitted or both are absorbed will be cos2q, while the probability that one is transmitted and the other absorbed will be sin2q. It was in 1964 that John Bell considered in detail these probabilities, and discovered a remarkable result, which has come to be known as “Bell’s Inequality”. He envisaged a series of experiments like the one described above, except that we are able to rotate the polarisers so that their axes may be set at any angle. Then, making a number of very reasonable assumptions, he showed that the results must obey this inequality, unless they were influenced by some strange effect such as the instantaneous transference of information from one photon to the other. He showed further that the results predicted by quantum theory did not obey the inequality, which would seem to confirm that such an extraordinary effect must be at work. The special cases considered earlier, with q equal to 0o or 90o, do not display these effects; they become evident only if we use a number of carefully chosen different values for q
.
9.07 The
final episode in this saga was written in the 1980’s, when improved
laboratory techniques made it possible for the first time to perform
some of the experiments which previously had existed only in
imagination. As expected, the results do confirm the standard formalism
of quantum theory; Bell’s inequality is indeed sometimes infringed by
the results of these experiments. So what is Bell’s theorem. and what
conclusions can we draw from the experiments which violate it? A
mathematical statement of the inequality can be found in many
textbooks, but the difficulty of fully understanding it and its
implications is increased by the fact that several different forms
exist, which at first sight are not the same. We shall not present any
of these forms here, but instead simply show the contradiction that is
revealed by one simple series of experiments using the apparatus we
have described above.
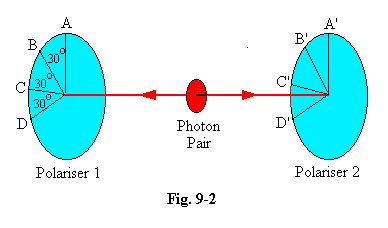
9.08 Suppose the optical axis of the polariser on the left can take any of the positions A, B, C or D, these being at 30 degrees to each other as shown, and those on the right, A', B', C' and D', are respectively parallel to them. For our first experimental run, set the axis of the left detector to direction A and the right one to B'. The angle between them is 30 degrees and so, as the above formula suggests, the probability of agreement is cos230o, or 3/4; with a sufficiently long series of readings, about 3/4 of the results at A, whether “yes” or “no”, will be the same as those at B'. Only 1/4 will be different, which means that the list of A results would need only 1/4 of them changing to give the B' results.
If instead of setting the left polariser to A it had been at C, while the right hand polariser remained at B', this in itself could not affect the run of results at B', which would be the same as before; we are assuming no non-local effects occur. And as the angle between the detectors is still 30 degrees, we would again find only 1/4 of the right hand results to differ from the left.
Thirdly, turn the right polariser to D', leaving the left one at C. Once again only 1/4 of the D' results will differ from the C results.
9.09 To summarise, only 1/4 of the A results differ from the B' results, only 1/4 of the B' results differ from the C results, and only 1/4 of the C results differ from those at D'. It follows that no more than 3/4 of the A results can differ from those at D'. But this is not what we observe; D' is perpendicular to A, and so all its results should differ. This contradiction is, in effect, an example of the sort displayed by infringements of Bell's Inequality.
9.10 What exactly is the significance of this infringement? The usual analysis goes something like this. Bell made two assumptions in deriving his inequality. The first was that no causal influences could be transmitted at a speed greater than that of light; we call this the locality assumption. Bell's second assumption was that the quantities we measure in quantum mechanics, in this case the orientation of the photons' axes, really do exist whether or not we attempt to make a measurement, the so-called reality assumption. So the fact that Bell's Inequality is broken, so the argument goes, implies that one or both of these assumptions, locality or reality, must be false. It is because the abandonment of either of these “obvious” precepts is so strongly opposed to intuition, that so much effort has been devoted to testing the EPR results experimentally, and to analysing the real implications of the results.
9.11 But
there is a damaging flaw in the argument we presented above. We omitted
an implicit stage in the discussion. We wrote, in effect, “With the
polarisers at A and B' the probability that the readings differ is 1/4.
So after a long run of trials, about 1/4 of the B' results will differ
from the A results. Similarly about 1/4 of the C results will differ
from the B' results." But we omitted to say, "Therefore no more than 1/2 of the A results can differ from the C results.”
Now this is meaningless, for there is a fundamental impossibility in
obtaining simultaneously a run of A results and a run of C results. We
cannot combine into one sample space the sample spaces corresponding to
the A and B' settings and the C and B' settings. The former has
possible values as follows:
A transmits B' transmits (prob = 3/8)The latter has possible values as follows:
A transmits B' absorbs (prob = 1/8)
A absorbs B' transmits (prob = 1/8)
A absorbs B' absorbs (prob = 3/8)
C transmits B' transmits (prob = 3/8)If we could design an experiment with all eight of the above results as alternatives, we could combine them into a single sample space, and find the probabilities of each of the eight possible outcomes. But A and C are not possible alternatives. No experiment could determine both the A results and those at C, for any determination of the photon's state by the A polarising filter will destroy the possibility of determining how it would have responded to the C filter. No combined sample space is possible, and the results at A are not related in any rational way with the results (in a different experiment) at C.
C transmits B' absorbs (prob = 1/8)
C absorbs B' transmits (prob = 1/8)
C absorbs B' absorbs (prob = 3/8)
9.12 We can express this differently. We claimed above that “if instead of setting the left polariser to A it had been at C, with the right hand polariser remaining at B', the run of results at B' would be the same as before”. This is a meaningless conterfactual. Philosophers have much difficulty in explaining the real meaning of counterfactuals, and the standard work on the subject, David Lewis’ book Counterfactuals (1973), leaves many questions unanswered, as I try to show in a publication on the internet (Conditionals and Counterfactuals, 1997). I believe any counterfactual in which the antecedent is not only false, but is essentially impossible, to be meaningless. This treatment of the EPR paradox provides a good example of such a meaningless statement. If the left-hand polariser is at A then it is fundamentally impossible to determine what the B' results would have been if the left polariser had not been at A. Under these circumstances I maintain that no meaning can be attached to the statement that "the run of results at B' would be the same as before", and once again we find that no conclusion can be drawn concerning the relationship of the A results to the C results.
9.13 So
far as we are aware, the only writer who has realised fully what the
observed infringements of Bell’s inequality do and do not imply is
Thomas Brody (The Philosophy behind Physics, Springer-Verlag, 1993). He shows that Bell implicitly made a third assumption in deriving his inequality, in addition to assumptions of realism and locality. He calls this the Joint Measurability Assumption. He writes:
The joint measurability assumption refers to the possibility of measuring two (or more) physical quantities without mutual interference; this last expression is to be understood in the sense that neither measurement affects the value obtained by the other... In the case of spin projections, the JMA is violated.He is referring here, of course, to the fact that a photon having passed through a polarising filter is supposed to be put into a new state, so that its original axis is no longer measurable. This is saying, in effect, what our own two statements above have said, that two measurements on the same photon cannot figure in the same sample space, or alternatively, that it is meaningless to discuss what result such an alternative measurement would have given if it could have been performed.
9.14 So the failure of Bell’s inequality in describing the results of EPR experiments tells us only that there must be an error in one (or more) of Bell’s three assumptions, reality, locality or joint measurability. As the last of these is false, we can make no deduction concerning the truth of the other two. The questions of the reality of measurable quantities, or the locality of quantum causality or influences, remain open, and we must look elsewhere to resolve them.
9.15 Although we are not forced to abandon either the principle of locality or of reality by the EPR experiments, because Brody presents us with a third alternative, it does seem that the probability which we associate with a particular photon being transmitted by a particular filter is inflenced in a non-local way by the orientation of the other filter, and by whether or not the twin photon is transmitted. Perhaps the two photons are governed by just one wave function rather than two, but some influence does appear to be transferred at superluminal speed. This can not be described as a causal influence, and it is insufficient to transfer information, and so infringe Special Relativity. The non-local influence on probabilities has no observable effect on any single pair of particles, for we cannot deduce the probability of an event merely by observing one instance of it; only when we observe a large number of particles do the effects of probability become evident. Indeed, no finite run of successive experiments, however long, can prove that the probabilities are influenced non-locally, any more than a run of "heads" when a coin is tossed repeatedly can prove that the coin is biased. But there is no doubt this influence exists, and it remains a strange phenomenon, with no parallel in everyday life.
9.16 We feel some discomfort when contemplating such non-local effects, even if they apply only to the probabilities of events happening rather than the occurrence of individual events themselves, but this discomfort is relieved to some extent by the Nodal theory. The most unpalatable aspect of the picture we painted is of the photon which has not yet encountered its polariser suddenly changing its spin axis because the other photon has encountered its polariser. Nodal theory teaches us, of course, that neither photon actually exists at this time, and all that is demanded is that, when the (imagined) photons reach their next nodes, the information fed into each node takes account of the orientation of the two polarisers, a picture which seems a little more credible.
9.17 Furthermore, as we have already shown, such non-local effects are an essential requirement of the nodal theory; indeed any particle in “moving” from one node to the next must “feel out” the whole of the surrounding region of space-time in order to “choose” its next node, and to determine what information is to be transferred to it. The present discussion extends this concept to cover the rather special circumstances encountered when a pair of particles become entangled, as they are in EPR experiments, and the behaviour of each is influenced by the region around both of them. So accepting the Nodal hypothesis means that our credulity is stretched no further by the EPR results than by other more common observations.
(c) Hector C. Parr (2002)
Previous Next Home Hector Parr's Home Page