Ch. 1
Ch. 2
Ch. 3
Ch. 4
Ch. 5
Ch. 6
Ch. 7
Ch. 8
Ch. 9
Ch.10
Ch.11
Ch.12
App.1
App.2
App.3
Biblio.
Index
Hector Parr's Home Page
Quantum Physics: The Nodal Theory
Hector C. Parr
Chapter 4: The Problems
4.02 The first question to be addressed in the new century concerned the radiation from hot bodies such as stars. The distribution of energy from such bodies and the way it depended on the temperature were well understood, but several attempts to derive these relationships by calculation failed. The failure was not just in the accuracy of the results; the answers obtained were nonsensical, showing that something fundamental was wrong in our understanding of the process of radiation. In 1900 Max Planck suggested a way out of the difficulty. He proposed that light was always emitted in small packets or quanta, the amount of energy in each quantum being proportional to the frequency of the light wave it contained. Symbolically, E = hf, where h is the constant number mentioned in Chapter 1. Calculation showed that this hypothesis led to exactly the right energy-curve, and the correct relationship with temperature. Planck's constant, h, could be calculated accurately, and was found to be a very small quantity, which explained why the effects of this quantised radiation of energy had not been suspected earlier.
4.03 This new theory became firmly established as it was found to explain with equal success some of the other problems associated with radiation. In 1905 Einstein applied it to the emission of electrons from the surface of a metal when light fell upon it, the photoelectric effect. The manner in which their energy depended on the intensity and wavelength of the light could not be explained by the old wave theory, and Einstein showed that quantum theory provided a full explanation. A few years later, Arthur H. Compton performed some remarkable experiments in which a block of graphite was illuminated by x-rays, and the wavelength of the scattered radiation was measured. Using Planck's energy formula, Compton showed that the energy of the scattered quanta depended upon the direction in which they moved just as if they had bounced off the atoms of graphite like billiard balls from the cushion of a billiard table. Here the x-ray quanta, or photons as they had been named, were behaving not like packets of radiation but like material particles.
4.04 Then in 1924, Louis de Broglie suggested that this dual nature of light, behaving sometimes like a wave and sometimes like particles, might apply also to material particles such as the electron. In fact he proposed that every particle of matter was associated with a wave when it moved. If v stands for the speed of the particle, and m its mass, the wavelength of the wave was given by the formula l = h/mv. This hypothesis was soon confirmed when diffraction and interference experiments were performed on electrons. Solid bodies behave, just as do light rays, sometimes as particles with precise positions and velocities, and sometimes as waves spread over a region of space, and having measurable wavelengths.
4.05 Two years later Erwin Schrodinger devised the equation which bears his name, and which describes the motion through space of the wave associated with any particle whose momentum and energy are known. At first Schrodinger believed that, when a particle needed to be described as a wave, it had become spread out throughout a volume of space, and the wave function which his equation gives us, and which he represented by the Greek letter Y, provided a measure at each point of the density of the distributed particle there. But it was soon realised that a much more satisfactory interpretation was obtained if Y was regarded as a measure of the probability density that the particle would be found at that point. The particle itself had not become dispersed, and the Y value at any point tells us just how likely we are to find it there. In fact Y is often a complex number, as we described in Chapter 3, and the associated probability density is given by the square of its magnitude, |Y|2.
4.06 As
understanding of sub-atomic physics improved, techniques were devised
for making accurate measurements on particles and waves. But it was
found impossible to devise experiments which would measure
simultaneously, with a high degree of accuracy, both the position and
the velocity of a particle. The greater the precision of one result,
the more inaccurate was the other. Then in 1927 Werner Heisenberg
discovered the uncertainty principle which is named after him.
He showed that these inaccuracies were not due to poor experimental
techniques, but that they were an inevitable result of the properties
of waves which, in other contexts, had been known for many years.
Suppose we know the position in the x-direction of a moving wave to a certain degree of accuracy, which we shall denote by dx. This means that the wave-packet has a length of dx,
and contains only a limited number of complete waves, as shown in the
diagram. Now it is known from general wave theory that such a packet,
because of its limited extent, must comprise not just one wavelength,
but a range of wavelengths which, by their mutual interference, can
limit the packet to a finite size.
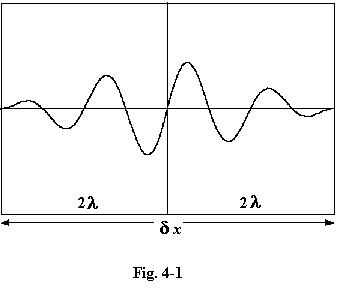
The fewer the number of wave crests within the packet, the larger the range of wavelengths which it must contain. The packet illustrated extends over about four wavelengths, and so it must be made up from a range of pure sine waves whose minimum and maximum wavelengths differ from the average by about one-quarter of this average. We know also the relationship between the de Broglie wavelength of a particle and its velocity, l = h/mv, and so the spread of wavelengths is a measure of our uncertainty of the particle's velocity. If we let p stand for the particle's momentum, which equals mv, we have l = h/p, and it is easy to show that, for the wave packet illustrated, the uncertainty of position, dx, and the uncertainty in momentum, dp, multiply together to give h. In general, any simultaneous measurements of position and momentum of a particle result in dx.dp being at least equal to h, and this is Heisenberg's principle.
4.07 Great progress was made in quantum physics during the first quarter of the twentieth century, but the problems and the perplexities were accumulating. How can an electron, say, be at the same time a particle, with a definite position and negligible size, and a wave, extending over a wide region of space? And how can we account for the fact that, if we wish to visualise the behaviour of a quantum system without actually observing or measuring it, we must follow the development of the wave, but whenever we make a measurement the wave appears to collapse, and a new wave is required to describe its future development? And what is the nature of the uncertainty which Heisenberg tells us is inherent in the system, and not just the result of poor experimental technique? Is the world not deterministic at the quantum level? Is it no longer true that identically prepared experiments lead to identical results, as they do in the world of common experience? Perhaps quantum effects really are deterministic, but we have not yet discovered the "hidden variables" which control them, in the same way that the hidden variables of standard mechanical theory control the motion of a spinning coin.
4.08 Early
in the development of quantum ideas Einstein and Bohr recognised very
clearly the dilemma posed by the dual particle/wave nature of quantum
objects, displayed forcefully by experiments where interference effects occur, effects that can be attributed only to waves. Bohr wrote as follows:
The [problem] is strikingly illustrated by the following example to which Einstein very early called attention and often reverted. If a semi-reflecting mirror is placed in the way of a photon, leaving two possibilities for its direction of propagation, the photon may either be recorded on one, and only one, of two photographic plates situated at great distances in the two directions in question, or else we may, by replacing the plates by mirrors, observe effects exhibiting an interference between the two reflected wave-trains. In any attempt of a pictorial representation of the behaviour of the photon we would, thus, meet with the difficulty: to be obliged to say, on the one hand, that the photon always chooses one of the two ways and, on the other hand, that it behaves as if it had passed both ways. (Discussions with Einstein, 1949)In the latter case, the production of interference fringes by using two mirrors, the photon always arrives at the screen as a single particle, and yet interference is displayed by the differing probabilities of its arriving at different parts of the pattern. For example it never reaches the centre of one of the dark fringes, and this shows that the wave must have been reflected by both mirrors. Which way has the actual photon itself gone? The depth of the mystery increases if we try to detect the photon while it is traversing the apparatus, for any successful attempt, whatever means we employ, shows that it has gone via one mirror only, but at the same time destroys the interference pattern. Nature will not reveal how a particle can perform an interference trick.
4.09 The “measurement problem” is really just another manifestation of this wave/particle dilemma. Because of the possibility that interference effects may occur, we must trace the behaviour of a quantum system between one “measurement” (or “observation”) and the next by means of its wave representation, often making use of Schrodinger’s wave equation. But the next observation seems to make the wave-function collapse, and the results of the observation always involve the new positions of particles rather than a new form for the wave. Unless and until another observation is made, no collapse occurs, and this has led some theorists to maintain that the very act of “looking at” a quantum system in some way determines its future development, as was described in Chapter 1.
4.10 The Copenhagen
interpretation is probably the most commonly held view on how these
difficulties can be resolved. Bohr acknowledged that the particle and
the wave were incompatible pictures of the quantum world, but
side-stepped the issue with his notion of “complementarity”. He pointed
out that our knowledge of the micro world could be obtained only
through experiments using macroscopic apparatus, and that any
experiment asking questions about particles could not be used for
waves, and vice versa, so at no time is a contradiction exposed by any one experiment. Thus an attempt to measure accurately the position of an electron (a “particle” experiment) rules out any prospect of measuring at the same time its momentum (which must involve a knowledge of its wavelength, requiring a “wave” experiment). Bohr writes about -
the impossibility of any sharp separation between the behaviour of atomic objects and the interaction with the measuring instruments which serve to define the conditions under which the phenomena appear. ... Consequently, evidence obtained under different experimental conditions cannot be comprehended within a single picture, but must be regarded as complementary in the sense that only the totality of the phenomena exhausts the possible information about the objects. Under these circumstances an essential element of ambiguity is involved in ascribing conventional physical attributes to atomic objects, as is at once evident in the dilemma regarding the corpuscular and wave properties of electrons and photons. (ibid.)Bohr rejected the idea of “hidden variables” on the grounds that, if they were essentially unobservable, they could play no part in a theoretical interpretation. He regarded the apparent indeterminacy of quantum phenomena as a fundamental component of their nature. And he maintained that the “collapse of the wave function”, when an observation was performed on a micro-event, occurred at the point in the causal chain between the event and the observer where an “irreversible amplification of the effect” had taken place.
4.11 An
alternative viewpoint, associated particularly with Eugene Wigner,
regards this point of irreversibility as too poorly defined to identify
something as clear-cut as the waveform collapse. His contention is that
the waveform continues to provide the only possible description of what
is happening right up to the point at which knowledge of an event
enters a conscious mind, which he claims is an occasion of much
greater certainty than an “irreversible amplification”. A more extreme
attitude to this question --
... has led Wigner and John Wheeler to consider the possibility that, because of the infinite regression of cause and effect, the whole universe may only owe its ‘real’ existence to the fact that it is observed by intelligent beings.” (In Search of Schrodinger’s Cat, John Gribbin, 1984)4.12 A number of physicists do not believe that this intervention of conscious minds is an essential requirement for the universe to be “real”, but subscribe instead to the “many universes” doctrine. David Deutsch describes it thus:
The idea is that there are parallel entire universes which include all the galaxies, stars and planets, all existing at the same time, and in a certain sense in the same space. And normally not communicating with each other. But if there were no communication at all there wouldn’t be any point to our postulating the other universes. The reason why we have to postulate them is that, in experiments on a microscopic level in quantum theory, they do in fact have some influence on each other. (The Ghost in the Atom, ed. Davies, 1986)The purpose of this theory is to circumvent the problem of the collapse of the wave function. Whenever a quantum system must choose between two states the whole universe splits into two, identical in all respects except that in one the first choice has been followed, and in the other the second. Each universe contains a separate copy of every conscious being, including you and me, complete with all our memories of the past, and each copy of us continues to live a separate diverging life, unaware of the existence of the other. In one version of the theory the number of universes continually increases as branching occurs, but in another version, all the universes already exist as indentical copies of each other, and a branching consists just of identical worlds becoming differentiated as a result of one quantum choice. Deustch subscribes to this view.
In my favourite way of looking at this, there is an infinite number of them and this number is constant; that is, there are always the same number of universes. ... When the choice is made, they partition themselves into groups, and in one group one outcome happens and in the other group another outcome happens. (ibid.)Thus, claim adherents to this view, is the problem solved of the wave-function collapse; it never occurs, but the different futures which the superposed waves decree are all pursued in different universes.
4.13 For some commentators the biggest challenge of the Copenhagen viewpoint is its indeterminacy, the fact that the future of a quantum system is not uniquely determined by its past history. There are, of course, many situations in the macroscopic world where we are unable to predict the future, but quantum indeterminacy is of a different nature; it is claimed that the data necessary for prediction just does not exist; quantum systems are intrinsically uncertain. Einstein was the most famous non-believer of this view. He maintained throughout his life that quantum theory was “incomplete”; there must be “hidden variables” which we had not yet discovered, and when we do understand them we shall, in principle, be able to predict the future of quantum systems as surely as we can preduct macro systems when we have the necessary resources.
4.14 Among
those physicists who do broadly accept the Copenhagen picture, there is
disagreement over the relative importance they attach to the
wave-function part of the picture, and the particle picture that
emerges when a measurement is taken. Roger Penrose makes it clear in
his writings that for him the wave is closer to “reality” than the
particle. He also stresses that the changing pattern of the wave-form
of a particle, as described by Schrodinger’s equation, is completely
deterministic, and he claims that it has nothing to do with
probabilities. He writes:
Regarding Y as describing the ‘reality’ of the world, we have none of this indeterminism that is supposed to be a feature inherent in quantum theory -- so long as Y is governed by the deterministic Schrodinger evolution. Let us call this evolution process U. However, whenever we ‘make a measurement’, magnifying quantum effects to the classical level, we change the rules. Now we do not use U, but instead adopt the completely different procedure, which I refer to as R, of forming the squared moduli of quantum amplitudes to obtain classical probabilities! It is the procedure R, and only R, that introduces uncertainties and probabilities into quantum theory. (The Emperor’s New Mind, 1989).
4.15 Now to present the writer's own views on these problems let us consider firstly the question of indeterminacy. What exactly would it mean if we did eventually discover, because the quantum world contains hidden variables of which at present we are unaware, that the world really is deterministic? It would mean simply that, given sufficient data and sufficient calculating power, we could use our knowledge of the past to predict accurately the future. But bearing in mind that the past and the future have no objective significance, and exist only in the minds of individuals in relation to their own “now”, of what importance is this matter of being able to calculate the events on one side of this arbitrary dividing plane from knowledge on those of the other side? To us, of course, it would be of immense importance. The biggest handicap we carry is the fact that our memory acts only backwards in time; it would be wonderful (or so it seems until we think about it deeply) if we could also remember the future! But to the universe at large it would be of little significance. There can be no question of the future being intrinsically indeterminate, in the sense that it is still open to alteration in a manner that the past is not, as we tried to show in Chapter 2. It is merely that we cannot see the future because our memory is not looking that way. If you give to an engineer a drawing of one half of an automobile engine, would he be able to complete the other half? He would probably make a good attempt at it; there is not much doubt where the main components would need to be placed, but on the other hand he might make some fundamental error; he might assume the distributor was driven from one end of the inlet camshaft, while in reality it should be the exhaust camshaft. Good fun, but not really important. And equally fascinating, but of no more importance, is the question of whether the future half of the history of the universe could be deduced from its past history. So it seems surprising that Einstein, who surely understood the nature of time better than anyone, should be so concerned about the apparent indeterminacy of quantum theory. He would probably have relented had he lived to see the EPR experiments conducted in the 1980’s, (which we discuss in Chapter 9), and the fact that even if the existence of hidden variables could remove the indeterminacy from quantum interactions, the non-locality revealed by these experiments would still remain.
4.16 Some aspects of Penrose’s view are puzzling. He gives priority of importance to the wave-function because it does not involve probabilities. “It is the procedure R [the process of making a measurement], and only R, that introduces uncertainties and probabilities into quantum theory”. But does this not overlook the fact that the wave is a probability amplitude? It was introduced by the quantum theorists in the 1920’s to describe the very probabilities which Penrose says do not exist. And his interest in the fact that U, the wave function, evolves deterministically between one measurement and the next, seems misplaced. U represents our best attempt to predict the future behaviour of a quantum system using the knowledge we have of its past; if U changes with time other than deterministically, then it can not represent our best effort. Until we have more information, any need to alter the prediction we have made, on the basis of information we already have, can arise only because we have made a mistake.
4.17 But the most telling objection to all the viewpoints we have described above is that they are not time-symmetric. The behaviour of any collection of particles is reversible, provided they are few enough for thermodynamical considerations not to apply. As the waveform is in essence a description of the particle's behaviour, it too should evolve in a way that can be viewed in reverse without breaking its own rules. The collapse of the waveform, whether we regard it as happening when a particle collision occurs, or when a measurement is made, or when a conscious mind knows a measurement has been made, is certainly irreversible, and indicates to us that the wave function, as understood in these theories, cannot be a part of physical reality, and can exist only in the mind of the observer. And the splitting of the universe into two is even more grotesquely irreversible.
4.18 The one fundamental principle which lies at the heart of all the perplexities of the quantum world is the fact that a quantum system, when faced with a choice between two or more different ways in which to develop, seems to keep all its options open until it is next observed. But what does this mean? The very idea is based on an assumption that, while the past is immutable, the future is undecided, an assumption which we hope the arguments of Chapter 2 have dispelled. When we view the history of such a system as a picture in the four dimensions of space-time, there is no dividing line between the past and the future, and both are drawn with the same firm strokes of the pencil. It is quite without meaning to claim that the future remains open while the past is closed. When this is accepted it becomes clear that a belief in this doctrine cannot reflect anything in the world outside our own minds. The uncertainty in the future of a system, and its apparent tendency to keep its options open, can be no more than a reflection of our own limitations. This does not provide an escape from the dilemma, but it does show that any way out proposed by the doctrine of an immutable past and an undecided future, is in fact just a cul-de-sac.
4.19 In recent
years a number of modified versions of the Copenhagen interpretation
have been developed which do reveal much deeper understanding of the
nature of time, and which acknowledge the need to describe
“time-symmetric” phenomena by means of a picture which is itself
time-symmetric. These deserve more attention than they seem to have
received. John Cramer’s “Transactional Interpretation” is carefully
thought out, and he describes it in his writings with admirable
clarity. He claims that it resolves some of the paradoxes which remain
with the Copenhagen picture, and in particular the unique and
questionable role performed by the observer. The essence of
Cramer’s model is the description of any quantum event as a
“handshake”, executed through an exchange of a normal “retarded” wave
and an “advanced” wave, which in effect acts “backwards in time”. Thus
if points A and B on the space-time diagram (Chapter 2, fig. 2-5)
represent consecutive events on the world-line of a particle, the
retarded wave acts from A to B, and corresponds closely to the wave
described by the Schrodinger equation. Then the advanced wave completes
the transaction by acting in reverse from B to A. Cramer writes:
This advanced-retarded handshake is the basis for the transactional interpretation of quantum mechanics. It is a two-way contract between the future and the past for the purpose of transferring energy, momentum, etc., while observing all the conservation laws and quantization conditions imposed at the emitter/absorber terminating ‘boundaries’ of the transaction. The transaction is explicitly non-local because the future is, in a limited way, affecting the past (at the level of enforcing correlations). It also alters the way in which we must look at physical phenomena. When we stand in the dark and look at a star a hundred light years away, not only have the retarded light waves from the star been traveling for a hundred years to reach our eyes, but the advanced waves generated by absorption processes within our eyes have reached a hundred years into the past, completing the transaction that permitted the star to shine in our direction. (An Overview of the Transactional Interpretation , International Journal of Theoretical Physics, 27, 227 (1988))
4.20 At first sight it appears that Cramer is making the mistake described in Chapter 2 and illustrated in Fig. 2-5. What is the difference between a wave starting at A and ending at B, and one starting at B and ending at A? We must remember that A and B are not points in space, but events in space-time, and that the movement of a particle from one point to another is represented simply by a line such as AB, and not by a point moving along AB. At each end of their trajectories the two waves occupy the same position and time; so they move together from one point to the other. Claiming that the advanced wave moves backwards in time is redundant and meaningless. But as one studies Cramer’s writing it is clear that he understands this perfectly. The only sense in which one wave goes from A to B and the other from B to A is that A is responsible for the retarded wave, and B responsible for the advanced wave. This question of responsibility or dependence is very difficult to define, and it does seem possible that Cramer’s model is unnecessarily complicated, and that indeed the advanced and retarded waves are different descriptions of the same entity. Even if this proves to be the case, however, the most valuable part of Cramer’s description concerns the transference of information, such as momentum and energy, between consecutive events on the world line of a particle. The idea that such information is transferred by the wave, and not by the particle itself, will become an essential feature of the Nodal interpretation which is developed in the remainder of this book. Cramer’s model is the first one we have examined which preserves the time-symmetry of the events it purports to describe.
4.21 Huw Price is another writer who believes that the mysteries of the quantum world can be explained if one is prepared to accept that, in some circumstances, earlier events can be influenced causally by later ones. Price is a philosopher, but his understanding of the subtle interpretation of physical principles is admirable, and every scientist with an interest in the fundamental nature of things should read his book “Time’s Arrow and Archimedes’ Point” (OUP, 1996). His analysis of the apparent “direction” of time, and of how one can avoid falling into the traps set by our deep-rooted intuitions concerning the flow and the asymmetry of time, is surely unsurpassed. Price believes in a form of “advanced action”, whereby the state of an incoming quantum system, as represented by its “hidden variables”, is influenced by the future setting of the apparatus which is going to perform a measurement. He shows persuasively that such a hypothesis can explain away the measurement problem, the superposition puzzle and its effect in interference experiments, and the EPR enigma, while preserving the idea of “locality”, that influences can be transmitted (in either time direction) no faster than light. The incredulity with which we react to suggestions that causal influences can act backwards in time is, of course, evidence of the power of our deep-rooted temporal prejudices, and should not preclude a careful appraisal of theories like Price’s. The micro-world is essentially time-symmetric; we accept that past events can affect the future, so surely there is no reason for us to reject the opposite, and Price mounts a robust defence of the idea. But is there a need for Price's theory? Its chief justification is that it abolishes the need for influences to transmit at super-luminal speeds, but why should this be so important? Einstein shows that neither particles nor information can travel faster than light, but the influences that are involved here are not of this kind, for they merely influence future probabilities rather than events themselves. We have no experience of such influences, and no direct way of knowing how they transmit, nor any reason to doubt that they can operate faster than light, so it seems to the writer that the “advanced action” hypothesis is ingenious but unnecessary.
4.22 Another book which handles the “arrow of time” problem with great insight is L. S. Schulman’s Time’s Arrows and Quantum Measurement (CUP, 1997). Schulman treats his subject matter more mathematically than Price, but he too resorts to a type of “backwards causation” to resolve the problem of the “collapse” of the wave function. When we believe the wave contains a superposition of different incompatible states, as in interference experiments, then the future measurement or observation we are about to make suppresses all the approaching superposed states except one; there is thus no need for a collapse to realise the one state that comes about.
4.23 These imaginative interpretations are to be welcomed. Contrary to popular belief, all the great discoveries of physics and mathematics are not made by deductive logical reasoning, but rather by flashes of imagination, which can then be supported deductively. Einstein was not the world’s greatest mathematician, but had remarkable powers of insight and visualisation, and it was these that led him to Special and General Relativity, his explanation of the photoelectric effect and other great discoveries. Almost equally brilliant were the insights of Bohr, de Broglie, Heisenberg, Schrodinger and Dirac during the first half of the twentieth century, from which the highly successful formalism of quantum mechanics has sprung. During the second half of the century there have on the other hand been a number of brilliant mathematicians, but they have done little to solve today’s problems in cosmology or particle physics, which are concerned more with interpretation than deduction, and demand intuition rather than logic. Indeed it has seemed that some of today’s mathematicians, far removed from the observatory or particle laboratory, have believed themselves to be solving the problems of the universe when all they were doing was shuffling symbols on a sheet of paper. As we enter a new century, can we hope that a new era of imagination and insight is dawning?
(c) Hector C. Parr (2002)
Previous Next Home Hector Parr's Home Page