Ch. 1
Ch. 2
Ch. 3
Ch. 4
Ch. 5
Ch. 6
Ch. 7
Ch. 8
Ch. 9
Ch.10
Ch.11
Ch.12
App.1
App.2
App.3
Biblio.
Index
Hector Parr's Home Page
Quantum Physics: The Nodal Theory
Hector C. Parr
Chapter 5: The Nodal Viewpoint
5.02 Chapter 1 put forward the view that any description of the quantum world should embrace two principles if it is to be accepted. Expressing these two principles more precisely, they are as follows:
1. Seen from the particle viewpoint, every fundamental sub-atomic process (with the apparent exception of the decay of the neutral kaon) is time-symmetric. This implies that, if the process is illustrated by means of a moving picture, and the sequence of frames is run in reverse, the behaviour will still appear compatible with all the laws of nature with which we are familiar. It follows that any model we adopt in order to visualise atomic phenomena, or any mathematical process we adopt to describe them, must also be time-symmetric. All the best-known current theories of quantum mechanics seem to fail this reversibility test.
2. A particle can have no influence on any other particle unless it encounters what we are calling a node. This may be a collision between two particles which subsequently rebound, or a collision in which the particles coalesce (sometimes called annihilation), or a splitting of a particle into two (sometimes called pair production). We can never observe a particle at a particular time and place unless it has a node there. The essential feature of the Nodal Interpretation is the proposition that a particle does not exist except at its nodes. We suppose that, while these nodes do have real existence, and precise positions in space and time, the particles we picture moving from one node to another do not exist. The trajectories which we imagine these particles to trace out between one node and the next have no counterpart in the real world.
5.03 The usual meaning attributed to the wave function of a particle is incompatible with this nodal viewpoint, for the wave is supposed to represent a probability distribution for the position of a particle while it is "in flight", and we are denying the existence of the particle in such circumstances. But with a slight change of emphasis a particle's wave function can continue to play a useful part in our description. The squared modulus of Y, integrated over a region of space at any given time, is said to give the probability that the particle lies within that region at that moment of time. Instead of this, from the nodal viewpoint we must say that, if the particle’s next node happens to occur at that given moment, then the squared modulus gives the probability that the node lies within that region. So |Y(r,t)|2 gives us, not the probability density that a moving particle occupies position r at time t, but rather the probability that, given that its next node occurs at the time t, its position will be r. Because of the time-asymmetry of our memories and of our record-keeping equipment, we often know something of the past history of a system, but not its future behaviour, and we try to predict this behaviour. Usually we can calculate only probabilities, whose values, it must be remembered, are essentially subjective, depending on the degree of knowledge we have of the past, and it is here that the wave function provides such a useful tool, even though it reflects our own biased view of reality as well as reality itself. But the Nodal approach insists that these probabilities do not refer to the particle’s position as it moves from one node to the next, but only to the position of that next node.
5.04 The particles which formerly we regarded as solid objects moving from node to node, we now claim to be fictitious, while the wave-form, in both its subjective and objective parts, consists of nothing more concrete than information. The nodes are the only substantial parts of this model, and indeed we assert that they constitute the only "material" things in the universe. So we must ask what are the properties of these nodes, and how we should visualise them. Each one has a definite position in space-time, corresponding to exact values of x, y, z and t, and under rather special experimental conditions we can sometimes determine these values with whatever degree of accuracy our methods of measurement will allow. It is only when the experimental set-up could give us some additional information about the momentum or energy of the (imagined) particles which come together at the node, that the degree of precision is reduced by the Heisenberg principle.
5.05 Each node must act as a "clearing house" for information relating to the particles, for there are restrictions on the possible relative positions which nodes can occupy, restrictions which can be enforced only by the interchange of information. In particular the positions of nodes in time and space must ensure that the (imagined) particles satisfy the conservation laws, such as the conservation of energy and momentum, and they must also pass on to subsequent nodes information about particle spin, electric charge, and the other properties which in the past we have attributed to the moving particles themselves.
5.06 Since, in this picture, we are denying the existence of a particle between one node and the next, we can no longer define its velocity as dr/dt, nor may we picture its speed as the swiftness of its motion, comparable with that of macroscopic objects like cars or planets. And yet we must still keep hold of the notion of momentum, for not only is momentum conserved in microscopic collisions, but the magnitude and direction of a particle's momentum is closely related to the wave picture which we have developed to describe a particle "in flight", as given by de Broglie's formula. Whatever place the wave function eventually holds as we develop nodal theory, it is clear that the concept of momentum, and hence of velocity, must continue to figure in our theory. We discuss this in a later chapter, but for the present we can show that in simple cases it does not present a stumbling block. Suppose a particle has a consecutive pair of nodes in free space, in a situation where previously we would have considered it to move between them in a straight line at constant speed. Because the x, y, z and t co-ordinates of the two nodes have perfectly definite values, there is no difficulty in defining the velocity between the nodes as (r2-r1)/(t2-t1), and this is the value which the nodes will "take into consideration" in ensuring that momentum is conserved there. It follows that, for a consecutive pair of nodes which lie in the past, there is no reason in principle why we should not know accurately both their positions in space and time, and the momentum with which the particle leaves the first and "arrives at" the second. The Heisenberg principle does not apply in such cases; it was pointed out in Chapter 1 that there has often been confusion concerning the situations in which the uncertainty principle does or does not apply. Our new approach changes the way in which we think about momentum, but does not change in any way the knowledge we can have of the momentum of a particle, or any of the results we expect from experiments.
5.07 The best way to represent quantum processes in diagrams presents us with a problem. It is easy to show the time and position of nodes on a space-time diagram, omitting, of course, one or two of the spatial dimensions because we cannot visualise or portray more than three. But how can we illustrate the relationships between nodes? We have seen that the trajectory of a particle from one node to another is not real, and this would seem to rule out drawing the usual Feynman diagram. But in general each particle preserves its identity through a series of collisions, and we can show this only by joining together in our picture the successive nodes visited by a particle, and the lines we draw are necessary also to illustrate the way in which energy and momentum are transmitted through a system, and conserved at each node. So it seems best to join up our nodes with straight lines, so far as the experimental setup allows; but it must be remembered that a straight line on a space-time diagram represents a particle moving with uniform velocity, and this is not the picture we should have in our minds.
5.08 There are many situations in which the lines connecting nodes cannot be straight, for instance when the "path" of a particle is diffracted as it "passes through" a small aperture. How is the disposition of nodes determined by the probabilities associated with different angles of diffraction? How, for instance, does a photon "know" that it may be diffracted through a large angle if the size of the aperture is small compared with the wavelength of the photon, but that this is unlikely if the aperture is larger? It is clear that, in some way, the relative positions of consecutive nodes are partly determined by the layout of all the matter in their vicinity, and that "knowledge" of this layout must be immediately available, with no restrictions such as that limiting transmission to sub-luminal speeds. Indeed, because the notion of simultaneity is denied by Special Relativity, this knowledge must encompass a whole region of space-time, past, present and future. We have here a generalisation of the "non-locality" revealed by the EPR experiments, wherein pairs of "entangled" particles show correlated behaviour which cannot be explained by sub-luminal transfer of information, as we shall discuss in a later chapter. The existence of non-local influences has gradually come to be accepted by proponents of all the differing quantum interpretations, for the results of these experiments have consistently refused to be explicable in any other way. We see now that such influences really apply much more widely, playing a part in determining the dispositions of nodes in all normal circumstances, and not only in the rather special situations met in EPR demonstrations.
5.09 We must stress that this purveyance of information throughout the whole of space-time does not imply the possibility of faster-than-light travel, nor does it provide a means of foretelling the future, or travelling into the past. We are material beings, composed of particles (or nodes) and restricted by all the laws of classical physics which particles obey. Claiming that these particles exist only when they collide does not change the laws which they obey. Although we must now regard the conservation of energy and momentum, and the restrictions of Special Relativity, as properties of the inter-relation between nodes rather than restrictions on moving particles themselves, these laws still apply. Anything we want to move from one place to another, and any information we wish to transmit, must be carried by the (imagined) particles of matter or radiation which we picture moving from node to node. It is the disposition of these nodes which ensures that particles of light or matter are still restricted in the speeds they can attain.
5.10 It
is interesting to compare this concept of nodes being "aware" of the
whole surrounding region of space and time with Feynman's "sum over
histories" picture. The value of this method lies not in its use for
doing actual calculations, for in most situations it would prove more
involved and tedious than the standard method using Schrodinger's
equations, but in the remarkably clear picture it gives of the
significance of these equations. J. C. Polkinghorne's description
cannot be improved upon; he explains here the sum-over-histories
approach to the well-known experiment in which a stream of particles
passes through two slits and produces an interference pattern on a
screen, as if it consisted of waves, not particles:
... Feynman tells us that we should think of all the different ways in which an old-fashioned electron with classically picturable simultaneous position and momentum could travel from the source through slit 1 and onto the specified point on the screen. There is obviously a vast number of such possible trajectories. ... Each is called a "path" or a "history" (both terms are used). Feynman tells us to consider all such possibilities and to assign to each a complex probability amplitude. It involves a quantity which physicists call action. ... Feynman next gives us a rule for associating a complex amplitude with this number. [For the learned it is exp(iA/h)] You then add together all the contributions from all the different parts and -- hey presto! -- the result is the same probability amplitude you would have calculated by the more pedestrian procedure of solving the Schrodinger equation. (The Quantum World, Penguin, 1984)
5.11 As an illustration of this method, Feynman shows that in open space a photon seems to travel in straight lines, and writes as follows. (In his simplified description, he uses arrows to describe the vectors or complex numbers which Y represents).
For each crooked path, ... there's a nearby path that's a little bit straighter and distinctly shorter -- that is, it takes much less time. But where the paths become nearly straight, ... a nearby, straighter path has nearly the same time. That's where the arrows add up rather than cancel out; that's where the light goes. (QED, p.54).
This clearly parallels closely the concept of nodes "feeling out" the whole of the space around them where adjacent nodes may lie. Such an "awareness" of the disposition of material bodies throughout the whole of the surrounding space-time must feature in any theory which claims to account for simple interference effects such as those observed in the "two slits" experiments.
5.12 What interpretation must we assign to Y in our theory? It was pointed out in Chapter 1 how clearly Heisenberg realised that the wave function is an unhappy amalgam of two sets of ideas, one objective and one subjective. How can we separate the two? The wave-function is clearly objective in that it encapsulates the identity of the particles whose trajectories we visualise as lines connecting one node with another, even though we acknowledge that these lines can mislead us by suggesting particles actually travelling through space as time progresses. And it is objective also in representing the information transferred between nodes to ensure that all the conservation laws are satisfied by their relative positions in space-time. But it is subjective in that it presupposes a moving time, and it is grossly time-asymmetric, for it is determined by the past nodes of a particle but not those lying in the future, reflecting the time-asymmetry of our own mental processes. This is most clearly seen if we consider a photon scattered from a material particle such as an electron. We have no idea in which direction the photon's next node will lie, and our ignorance is represented by the expanding spherical wave which we imagine to radiate outwards from the source, only to "collapse" when we know the whereabouts of the next node. If, by some miracle, we could know the position of the later node, but not the earlier one, then our probability wave would have to converge on the former rather than radiate from the latter. This alternative situation is not as bizarre as it may seem, and has been considered in detail by some physicists; they refer to such converging waves as advanced, to distinguish them from the more familiar retarded waves of every-day experience. We shall devote a later chapter to consideration of these two kinds of radiation. For the time being we must be satisfied with the dictum that those aspects of the wave function which are asymmetric in time are subjective, and assume that those which are symmetric are objective. We can visualise the objective features of the wave as providing the information linkage between nodes, but our picture is still imperfect if it suggests that the information "travels" from one node to the next, and that there is a preferred time direction.
5.13 We shall quote
Heisenberg again, showing his understanding of the dual nature of the
wave function, the subjective and the objective. Writing about the
motion of an electron, he wrote:
The probability function ... represents a fact in so far as it assigns at the initial time the probability unity (i.e., complete certainty) to the initial situation: the electron moving with the observed velocity at the observed position ... It represents our knowledge in so far as another observer could perhaps know the position of the electron more accurately. ... When the probability function has been determined at the initial time from the observation, one can from the laws of quantum theory calculate the probability function at any later time and can thereby determine the probability for a measurement giving a specified value of the measured quantity. (The Copenhagen Interpretation of Quantum Theory, ch.3).
5.14 We see that the wave function represents in part facts about the quantum world it purports to describe, but at the same time incorporates information about an observer’s knowledge of this world, knowledge which forms the basis of the probability predictions he can make, but which is purely subjective in that different observers may use different functions to describe the same phenomena.
5.15 In what follows we shall often need to distinguish between the standard wave function of quantum mechanics, with its combination of subjective and objective features, and the more restricted objective, time-symmetrical wave, which contains no features pertaining to our knowledge of a system. Throughout the rest of these pages we shall refer to the former as the conventional wave function (which we abbreviate to CWF), and the latter as the nodal wave function (which we abbreviate to NWF).
5.16 It is important to have in the imagination some picture of the world which takes into account everything we do know about quantum theory. Such a picture may play no part in the calculations which predict the outcome of experiments, and nor will it affect any deductive argument we conduct in attempting to develop our theories. But it can act as a valuable stimulus to the imagination, and so can have a powerful influence on the inductive arguments we present to ourselves when thinking about these theories. Our picture must be time symmetric, for we have agreed that the sub-atomic world, and any description or representation we give of this world, must continue to make sense if the direction of time is reversed. But we know that the idea of a moving picture or a moving time is itself invalid; if we view quantum processes in this way we are imposing on the system something that is subjective and illusory. The only way to be sure we are not thereby reaching false conclusions is to picture a static four-dimensional world, and to strive constantly not to allow any change or movement to impose itself on that picture. On this framework we can visualise a distribution of nodes representing the whole history of the universe, or more realistically a small part of this history. We are very tempted to picture our "now" plane moving upwards, to show our imagined “flowing” of time, but we must suppress this false picture. Equally importantly, there can be no question that events above this plane are in any way less real, less substantial, or less determined, than those below it. The distinction between the past and the future is purely within our own brains, and exists only because we can remember the past but not the future.
5.17 We may picture our nodes connected together by lines, not to indicate the trajectories of the particles, but simply to represent which particles are involved at which nodes, and to display the imaginary channels along which information is shared. Here again we must not see the information as flowing along these lines, either in one direction or the other. The nodes are just there, and the information shared beween them is just there also.
5.18 The
nodes are not distributed at random. An important part of the
information which they share with one another ensures that their
positions in space-time obey the laws of conservation of momentum and
energy. It is instructive to examine in detail a simple situation such
as a collision between two particles in free space. This is illustrated
in the diagram, and it will be seen that five nodes are involved.
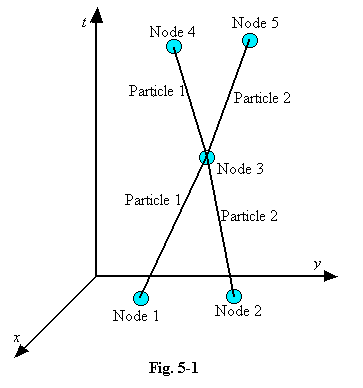
The position of each one of these contributes something to the information exchanged at the node marking the actual collision, for we define the momenta of the particles arriving at node 3 in terms of the positions of nodes 1 and 2, and the momenta of the particles leaving node 3 in terms of nodes 4 and 5. To describe the positions of the five nodes would require twenty co-ordinate values (since our diagram represents a four-dimensional space). But these twenty values are not independent. We can write down three equations describing the conservation of momentum at node 3, and one for the conservation of energy. As a result the conservation laws reduce the number of degrees of freedom of the five nodes from 20 to 16.
5.19 We should examine further the effect of these conservation laws, for they throw light on one of the chief sources of quantum determinacy. Consider firstly a familiar problem in classical dynamics. If we are given a pair of smooth, perfectly elastic spheres colliding in three dimensional space, it is possible to calculate accurately the two velocities after the collision. We have six unknowns, the three components of the velocity of each sphere after the collision. And we have six equations; the conservation of momentum gives us three, conservation of energy gives one, and the fact that the relative velocity of the spheres in the plane perpendicular to the line of centres at the moment of collision is unchanged gives us two more equations. But in order to use this last fact we must know the orientation in space of this line of centres. Comparing this situation with the collision of two elementary particles, the conservation of momentum and energy again give us four equations, but there is no information analogous to the orientation of the line of centres at the moment of collision, which is meaningless for bodies of infinitesimal size. So we lack two equations, and cannot calculate the final velocities, however much we know about the state of affairs before the collision. We see that, at every collision of elementary particles, from the six degrees of freedom which the final velocities possess, two of these are indeterminate.
5.20 If there is difficulty picturing a set of nodes, fixed in space-time, with some restrictions on their possible disposition, but with the information required to define these restrictions fixed also, and not being transmitted from node to node (which would involve some change in our four-dimensional picture), perhaps a little children's experiment in two-dimensions may help. Many of us have tried magnetising a number of needles, pushing these vertically into corks, and floating them in a basin of water. The needles repel each other, and they move into one of a number of possible positions of equilibrium. If we view this situation after the needles have taken up their final positions, their magnetic fields clearly influence their possible positions, but is not moving from needle to needle; in a comparable way, the nodes have fixed positions in space-time, with information imposing restrictions on their arrangement, but without any flow or movement of information being needed. Although this is an imperfect analogy, it may help us imagine a system of nodes in space-time, and their interaction.
5.21 But what corresponds in the quantum world with these magnetic forces in our model? What is the medium through which nodes influence each other? We attribute this influence to the Nodal Wave Function (NWF), but of its true nature we have no idea. Whether we shall ever understand the fundamental laws at a sufficiently deep level to answer this question is a matter for surmise and discussion. All we can do at the present time is to catalogue systematically the effects which these laws have on the nodes themselves. In the first place they decree that some arrangements of nodes in space-time are not allowed because they do not obey the rules of conservation of momentum and energy, and in a more complicated way, those other rules related to electric charge, angular momentum and phase information. Of those arrangements that are possible, some occur more frequently than others, giving us the probability element which our previous pictures of the quantum world have incorporated. We have seen that the nodal part of the wave function of a particle, the NWF, does really exist in some sense, and it is this which links together the nodes in any region of space-time, and "carries" the information which connects consecutive nodes along the (imagined) world line of a particle.
5.22 The reason behind the Heisenberg uncertainty principle, as it applies to position and momentum, can be clearly seen by considering a typical example. The only things we can observe directly are nodes, such as the collision of a photon with a photographic plate, and the only direct information we can gain from such an observation is the position in space and time of that collision. We cannot observe the wave form as it carries information from one node to another unless we introduce a new node, and we can discover facts concerning the energy or momentum of a particle as it arrives at our detector only by some kind of subterfuge, for example by introducing additional apparatus. And this additional information can make itself known to us only by changing the position or time of such a collision.
5.23 Suppose
we want to know where a photon strikes an opaque screen, and find out
also the direction from which it came (this latter representing momentum
information). We could make a small hole in the screen, and place a
photographic plate a small distance behind it. When a photon "passes
through" the hole we know its position as accurately as the hole in the
screen allows, i.e. with an uncertainty of dx, where dx
is the diameter of the hole, and the mark it makes on the photographic
plate should show us the direction from which it approached the hole.
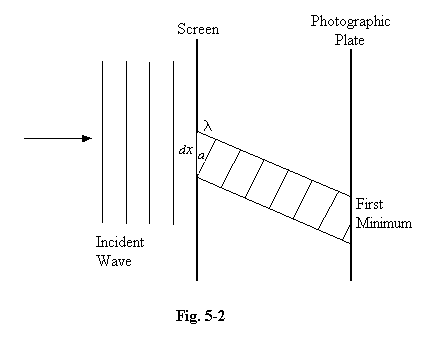
But in passing through the hole, the particle is likely to deviate from
its straight course because of diffraction. In other words the momentum
in a direction parallel to the screen, p, will suffer a change of unknown magnitude, dp,
and this will introduce an uncertainty in our determination of
momentum. A simple geometrical argument can give us the likely range of
values this change will adopt, and shows that our uncertainty of the
particle's position and momentum at the screen obeys the Heisenberg
relation, dx.dp > h.
[For those who want the mathematics:
The probability that the particle reaches a particular point on the screen depends upon the angle a. The diagram shows the angle for which the first minimum occurs, when that part of the wave coming from the top of the aperture gets ahead of the part passing close to the bottom by one complete wavelength, and all possible phases are combined in the resulting wave. These will largely cancel each other, and we get a band of minimum brightness on the photographic plate, and the angle a can be taken as the characteristic angle of diffraction for this wavelength. We see that sin a = l/dx and a simple "triangle of velocities" shows that dp = p sin a. So dp = pl/dx or (h/l) X (l/dx). We derive immediately dx.dp = h.]
5.24 Diffraction effects such as this are very real; the pattern on the photographic plate confirms that they have occurred. So the waves we have envisaged at the hole in the screen must really exist; they belong to the NWF as well as to the CWF. We shall examine in detail the form taken by the NWF in simple cases in Chapter 11.
5.25 Interference effects, such as those produced by the famous “two slits” experiment can now be explained. There was never any difficulty understanding how these effects are generated by waves; they were discovered and explained long before the quantum was thought of. The problem lies in explaining them when a beam of light is treated as a stream of photons. If each photon were to pass through both slits it must divide into two; but this cannot be the case, for each would then have only half the energy, and twice the wavelength, of the incident photons, giving the wrong interference pattern. We now know the answer: the photons, regarded as particles, do not exist. They pass through neither slit; it is the wave which passes through both slits.
5.26 The troublesome collapse of the wave when an observation is made can now be viewed in a different light, when it is recalled that this aspect of the wave, because of its time-asymmetry, must belong to its subjective or conventional features. It exists only in the mind of the observer, and owes its form to our own ignorance of the future, an ignorance we can do nothing to relieve until we make another observation. It inevitably changes discontinuously when such a measurement results in additional information entering that mind. The "collapse" of the wave-function when we gain further knowledge of the system is no more surprising than the collapse of our anticipation when we learn that the winning number in a lottery is, or is not, the same as the number on our ticket. It must be admitted, however, that this is a rather facile dismissal of a problem which has troubled thinkers for a hundred years, and we shall attempt a more detailed analysis in Chapter 12.
5.27 Perhaps the most difficult concept which the Nodal Theory forces upon us is its non-locality. The information transferred between nodes must take into account the content of the whole of the surrounding region of space-time, including points which can not be reached at sub-luminal speed, and even points representing the future. But as explained above, the concept of non-locality has already been taken on board by all schools of thought in the quantum debate on the EPR phenomena. The writer believes that each of the other quantum interpretations stretches our credulity further than does this concept of non-locality, and herein lies the main reason for advocating the nodal view in preference to the others.
(c) Hector C. Parr (2002)
Previous Next Home Hector Parr's Home Page