Hector Parr's Home Page

7.02 Momentum enters into the Nodal picture in two guises, neither of which bears any likeness to the momentum of the classical physicist. The characteristics of momentum in Newtonian physics are motion and mass, the sort of things we are aware of if we are struck by a moving object, or are trying to move one that is stationary. In Nodal quantum physics the idea of moving particles plays no part, while mass is no more than a component of the information which forms the linkage between nodes. Furthermore, as we have shown, the concept of velocity is now abstract, being no more than the result of a division sum; in simple cases where we can think of particles “moving” from node to node in straight lines, we obtain velocity by dividing the distance between a pair of nodes by the time separating them. The momentum of the particle is found by multiplying this result by the particle’s mass. The alternative representation is no less abstract. The wave-function which we imagine spanning the interval between these two nodes has an oscillatory character, and de Broglie’s rule shows that the wave-length of the oscillations is a direct measure of the momentum of the particle it represents; in fact momentum = h/l, where l is wavelength and h is Planck’s constant. The Nodal theory does not specify what degree of physical reality we should ascribe to the wave-function, but its usefulness in calculation is unquestioned.

7.03 Despite the different nature of momentum in the Nodal theory, the way in which the concept arises in the discussion of quantum processes is often very “classical”. An early example was provided by the Compton effect, discovered by A. H. Compton in 1923. When X-ray photons are scattered by the free electrons in a block of graphite, the scattered photons are found to have their wavelength (and hence their momentum) changed to an extent that depends upon the angle of deflection. The results confirm that energy and momentum are both conserved as they would be in the collisions of elastic macroscopic bodies. Niels Bohr wrote about the effect as follows:

This phenomenon afforded, as is well known, a most direct proof of the adequacy of Einstein's views regarding the transfer of energy and momentum in the radiation process; at the same time, it was equally clear that no simple picture of a corpuscular collision could offer an exhaustive description of the phenomenon. Under the impact of such difficulties, doubts were for a time entertained even regarding the conservation of energy and momentum in the individual radiation process; a view, however, which very soon had to be abandoned in the face of more refined experiments bringing out the correlation between the deflection of the photon and the corresponding electron recoil. (Discussions with Einstein, 1949).

7.04 The first of our problems arises as soon as we consider in more detail the simple “motion” of a particle from one node to the next in free space. If we know the particle has been emitted at a point A, but have no additional information, from our point of view the wave-function will radiate spherically from A. But the other particle involved in the collision at A must suffer a recoil equal and opposite to the momentum change in the emitted particle. How can this happen if the direction of this momentum is not yet determined? And if the emitted particle travels a great distance before its next collision, its momentum could be indeterminate for an extended period of time.

7.05 Einstein and Bohr considered this problem in their historic discussions. Thus,

... Einstein stressed the dilemma still further by pointing out that the argumentation [of quantum theory] implied that any radiation process was ‘uni-directed’ in the sense that not only is a momentum corresponding to a photon with the direction of propagation transferred to an atom in the absorption process, but that also the emitting atom will receive an equivalent impulse in the opposite direction, although there can on the wave picture be no question of a preference for a single direction in an emission process. (ibid.)

7.06 The Nodal picture appears to exacerbate this problem. Not only is the direction of the particle’s “trajectory” unknown, but we are claiming that the particle does not exist between its emission and absorption, and so its momentum must be missing from the system during this period. If it is (mistakenly) assumed to travel from A to B, then the centre of gravity of the whole system undergoes no change of velocity. But if we deny the existence of the particle between A and B, then both at the instant of emission and the instant of absorption, the momentum of this complete system suffers an instantaneous change, and between these two times momentum appears not to be conserved. Like so many problems, however, this one vanishes as soon as it is looked at from the correct viewpoint. We should be viewing the interaction of these particles as a static four-dimensional pattern of nodes in space-time; any picture we have of particles “moving” on this pattern, carrying momentum with them, must not be allowed to affect our understanding of the real world. The conservation of momentum is not concerned with the interactions of moving massive bodies; rather is it a rule restricting the possible positions of nodes in space-time. Some apparently possible dispositions of nodes do not satisfy these restrictions, while other do. All the arrangements which we find in practice are such that momentum is conserved. As the only information we can gain from a system is obtained by observing the space-time positions of these nodes, we never observe breaches of the conservation laws, for these occur only between nodes; the deficit existing during the “travel” of a particle is always restored on its “arrival”.

7.07 The Heisenberg uncertainty does not prevent us from calculating accurately, in principle, the momentum of a particle between any pair of nodes lying in the past. There is no element of intrinsic uncertainty in the location of the nodes themselves in space-time, and, when referring to past collisions, there is no limit to the accuracy with which we can measure their positions and times of occurrence, and hence no limit to the precision with which we can describe the momenta of particles between collisions. We give two illustrations of methods by which the positions of a pair of past collisions can be determined experimentally to whatever degree of accuracy our techniques allow:

1. Suppose we wish to know accurately the points of emission and absorption of an electron in a vacuum tube. We can release a brief burst of electrons from position A at time t_A. Then if one of these is detected by a flourescent screen at B, there is no fundamental restriction on our knowledge of the positions A and B, or of the times t_A and t_B. So the velocity between A and B can be found, and the momentum determined.

2. A different procedure must be adopted for photons. Unlike an electron, a photon does not possess a rest-mass, but on the other hand, we do always know its speed of travel (using the old language of “moving” particles). Limiting the duration of the emission of a burst of photons would lead to uncertainty in their energy, and hence their momenta, because of the Heisenberg effect. But in this case we can use a source of known wavelength, and allow a long burst to be emitted to minimise the uncertainty. When one photon is detected at B at time t_B we can use our knowledge of the velocity of light to calculate the exact time t_A of emission, and so again we can find accurately the position and time of this photon's emission and absorption.

7.08 Perhaps more troubling to the quantum physicist whose training was rooted in the classical tradition, is the realisation that the wave-function radiates in all directions from the emitting atom, and yet the photon which it represents seems to "know" in which direction to go in order to reach its next node, for this direction must be opposite to the emitter's recoil. We must remember, however, that the “radiation” of a wave-form is merely a picture necessitated by our prejudiced viewpoint; we may know the location of event A, but until B occurs we cannot know its location or time. The “real” wave between A and B, the NWF, cannot incorporate this feature of radiating from A, for it must be time-symmetric. If our mental moving picture of what is happening looks less reasonable when run in reverse, we know it must be wrong. In fact the NWF "knows" the location of B, and so does not need to radiate outwards searching for it. We shall consider the apparent asymmetry of radiation in greater detail in Chapter 8, and in Chapter 11 we will examine the general form taken by the NWF in some simple situations.

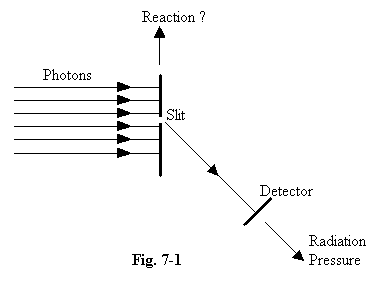
7.09 The next problem we consider occurs with an experimental arrangement in which photons of light fall upon an opaque diaphragm containing a narrow slit. The emerging light will be diffracted, and if a light-sensitive device is placed off-centre to observe photons which have apparently changed direction on passing through the slit, we seem to have a momentum paradox. When the experiment is conducted macroscopically, involving a large number of photons, the detector will clearly receive all its light from the direction of the slit, and will experience an impulse due to radiation pressure. This can not be balanced by a reaction on the light source, for all the photons which reach the detector have started their "journey" in the direction of the slit, and their reaction on the source must be opposite to this. The classical explanation demands a reaction between the photons and the diaphragm, for it is here that they change direction in passing through the slit. Bohr and Einstein considered this question in detail in their discussions in 1927. From the record which survives of these discussions it seems that both men assumed implicitly that indeed there is a transfer of momentum between the photon and the diaphragm; their disagreement was only about the possibility of measuring this transfer. Einstein at first was sure such a measurement would be possible, but had to accept Bohr’s argument that it is not. Bohr shows that the uncertainty principle must be applied to the diaphragm as well as to the particle. He writes,

Here, it must be taken into consideration that the position of the diaphragm has so far been assumed to be accurately co-ordinated with the space-time reference frame. This assumption implies, in the description of the state ... an essential latitude as to its momentum. However, as soon as we want to know the momentum ... [of the diaphragm] with an accuracy sufficient to measure the momentum exchange with the particle under investigation, we shall, in accordance with the general indeterminacy relations, lose the possibility of its accurate location in space. (ibid.)

7.10 The Nodal picture of the situation is different. Firstly it must be pointed out that the diffraction effects are not produced by photons colliding with the edges of the slits; if they were, the resulting distribution of light, and its dependence on the width of the slit, would both be entirely different from what is observed. The diffraction is due to the diaphragm shielding the off-centre regions from any direct radiation, radiation which, if present, would cancel the diffracted beam, as described so well by Feynman’s “sum over histories” picture. So if we consider a single photon, it is clear that it cannot suffer a collision at the slit; only the wave passes through the slit, and its change of direction is due to the absence of the waves on either side which would neutralise any wave moving in the “wrong” direction. Such a photon therefore cannot transmit any momentum to the diaphragm since it does not have a node there. Indeed the Nodal theory denies that it passes through the slit; it does not exist between the source and the detector.

7.11 But does this not lead to a contradiction in the case of the macroscopic experiment which we described at first, where a beam consisting of very many photons falls on the slit, and the light-sensitive detector placed off-centre experiences a light-pressure with a sideways component from those photons which are diffracted in its direction? No, there is no contradiction, because the photons which actually strike our detector are an unrepresentative selection of the set of photons which "pass through" the slit. In fact photons are diffracted to the right and to the left in (very nearly) equal numbers; the sideways component of the force on the off-centre detector will be balanced by the force exerted by those photons which are deflected in the other direction, and impinge on some other part of our apparatus. The nodal theory predicts here another microscopic breakdown of the conservation law, but of a magnitude which is essentially unmeasurable.

7.12 The above argument, that a photon deflected by diffraction will not exert a reaction on the apparatus which causes the diffraction, can not be applied, however, when a ray of light is reflected from a mirror. Here the change of momentum of all the photons is in the same direction, and can therefore be detected macroscopically; a stream of photons does exert a measurable force on a mirror which changes its direction. This can only occur if the photons experience real collisions with the particles constituting the reflecting surface. The question to be answered now is how these photons can retain their coherence despite these collisions. We saw in the previous chapter that the interference is lost in “two-slit” experiments if the photons suffer collisions as they pass through the slits. Interference effects can also be observed when a beam is split by a half-silvered mirror, and the two halves are brought together again by two fully silvered mirrors; why does the collision which a photon experiences at such a mirror not influence its coherence in the same way as is suffered by photons which are detected going one way or the other in two-slit experiments? The reason can be found in the fact that the molecules of a rigid solid such as a mirror are held tightly together by the rigidity of the solid. To act as a (theoretically) perfect mirror a surface must be infinitely massive and rigid, for it reverses the normal component of the momentum of the incident photons without affecting their energy, and so can not experience any recoil movement. It follows that the momentum of each photon can be changed in direction without any change of speed. A single photon gives up no information to such a fixed mirror, apart from that relating to the change in direction of its momentum, and so is still able to produce interference effects. Furthermore, although it has imparted some momentum to the mirror, we cannot detect this for a single photon, for to do so would require us to allow the mirror to move by a sufficient margin to destroy the interference. So just as in the comparable two-slit experiments, a stream of photons which has been spilt in two can be brought together again by mirrors to cause interference effects. As in the two-slit case, it is impossible to determine which path an individual photon follows without at the same time destroying the interference.

7.13 But this requires further consideration. In the two-slit case we asked whether each individual particle passed through both slits, through neither, or through just one. The Nodal theory gave a clear answer: they pass through neither. In the case of mirrors, however, each photon must experience a collision to change its momentum, and so has a node at the point of reflection. Each photon must follow just one of the two possible routes through the equipment. The associated wave-form is “aware” of both routes, and it is the interference of the two waves which ensures that the photon arrives at a particular point of the interference pattern with the required probabilities. One mirror reflects just the wave-form itself, while the other introduces an additonal node, and a real collision of particles. No phase information is lost at either mirror, and as it is impossible to discover which route a particular photon has followed, the situations really are virtually symmetrical, with both routes contributing equally to the information delivered at the screen.

7.14 It is easy to see why interference will be lost if a successful attempt is made to determine which of the two paths the photon really follows, by looking for the recoil of one of the mirrors. The mirror must be able to detect a momentum change of the order of p = h/l, and so it must be free to move. By the Heisenberg principle its position is indeterminate to within h/p, i.e. the photon's wavelength, and this uncertainty destroys the interference effects. Both the momentum of the photon and the length of its path are changed, so that the coherence of the two waves is lost.

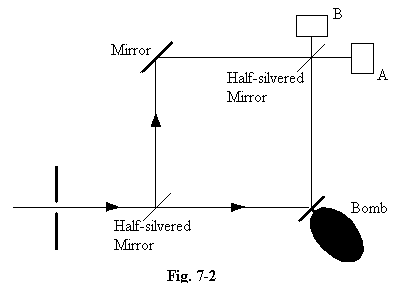
7.15 Penrose describes an amusing thought experiment (Roger Penrose, The Large, the Small and the Human Mind, CUP, pp.66-70) in which a bomb is detonated by the movement of a small mirror, so sensitive that it will respond to a single photon. If some such bombs are faulty, with their mirrors jammed, it would appear impossible to pick out the good bombs without detonating them, for the only way of detecting a good bomb is by moving its mirror. But suppose we use the bomb's mirror in one arm of an interferometer. Photons are sent through the apparatus one by one, and if the bomb has a jammed mirror then interference will take place, and some points on the screen will be inaccessible to the photons. In the arrangement that Penrose describes, a second half-silvered mirror is placed where the two beams re-combine, in such a way that all the photons will arrive at a point A if interference occurs, but if there is no interference some photons will arrive at A and some at B. So photons can reach B only if interference is suppressed, showing that the bomb is a good one, with its mirror free to move. In these circumstances Penrose maintains that only one in two of such bombs will be exploded by the test, for there is an equal probability that the photon will travel by the other route and be reflected by the fixed mirror. The wave will then detect that the bomb’s mirror is free, but because the photon itself goes by the other route, the bomb's mirror will not be moved and it will not explode. In this way, Penrose claims, it is possible to pick out some of the good bombs without detonating them. The experiment tells us what would have happened if the photon had been reflected from the bomb’s mirror.

7.16 It seems that this device would operate in principle as Penrose describes, but let us examine in detail the underlying reason. Notice firstly that, if we are to be certain a dud bomb, with jammed mirror, will never actuate the B sensor, we must set up the interferometer with “zero tolerance”. If the position of the bomb’s mirror differs from its correct position, even by a small fraction of l, then the probability of a B result will increase, and will oscillate between 0 and one-half as the error in the bomb’s position increases. Secondly, because the mirror of a good bomb must act as a measuring device, able to detect an impulse as small as p, by the Heisenberg principle the position of its mirror must be uncertain to within a distance h/p, i.e. l. So as we wheel in a good bomb, we shall be unable to position its mirror to within this distance of the correct position, and it is this geometrical inaccuracy, rather than any mystical effect of the wave-form on the movable mirror, which makes possible detection of the photon at B.

7.17 So Penrose’s astonishment at the result is misplaced. He writes,

It is quite extraordinary that quantum mechanics enables you to test whether something might have happened but didn't happen. It tests what philosophers call counterfactuals. It is remarkable that quantum mechanics allows real effects to result from counterfactuals!

No, it isn’t really so remarkable. We designed the equipment so that, when we detect that a photon has passed through, we know it must have been reflected from one of the two mirrors. If it arrives at point B, showing that interference has not occurred, we know the geometry must be wrong, while the failure of the bomb to explode proves the photon was not reflected there, so it must have been reflected from the fixed mirror. In the same way we manufacture coins with a “head” on one side and a “tail” on the other. Is Penrose astonished, when he looks at a coin, that he knows what he would have seen if he had looked at the other side?

7.18 We have examined just a few of the implications for nodal theory of the transfer of momentum in atomic experiments, and have had some surprises. In particular, the conservation of momentum, long held to be a universal law of nature, is found to be broken on the scale of single atomic particles, but only to an extent that is fundamentally unmeasurable and undetectable, and in situations which cannot result in macroscopic deviations from conservation. This explains why we have never encountered such discrepencies in experiments, and ensures we shall never do so.

Previous  Next  Home                    Hector Parr's Home Page