Ch. 1
Ch. 2
Ch. 3
Ch. 4
Ch. 5
Ch. 6
Ch. 7
Ch. 8
Ch. 9
Ch.10
Ch.11
Ch.12
App.1
App.2
App.3
Biblio.
Index
Hector Parr's Home Page
Quantum Physics: The Nodal Theory
Hector C. Parr
Chapter 11: The Nodal Wave Function
11.02 This picture of an electron's wave packet does bear some relationship to reality. If we imagine (falsely) that the particle travels in a straight line at constant speed, its position at any instant should lie within the limits of the moving wave, and the true wavelength of the particle will lie within the limits set by the uncertainty principle. But in several respects the picture is false, for the spread of wavelengths, and the associated limited length of the wave packet are due solely to our own limited knowledge of a particle whose future history we do not know. The positions in space-time of the two nodes are perfectly definite, so there is no intrinsic uncertainty in the momentum, but the movement of the wave packet from node to node does not represent anything in the real world, for the electron does not really make the journey. Because the waves represent the electron's probability amplitude, however, the wave function does indicate to us the probability, based on our present information, that the particle's next node, if it occurs at the moment represented in the picture, will lie within the packet. We can imagine the packet moving along to the right in our diagram, and preserving the same wave structure as it moves, but here again we are in error. Mathematical analysis shows that the average speed of the packet is indeed v, as we would expect, but the waves themselves, as distinct from the packet, move at a different speed. In fact the waves are moving through the packet with speed c2/v, where c is the speed of light. (For a simple derivation of this result see Modern Physics, by Gautreau and Savin, pub. McGraw-Hill, p.80.) This speed is usually far in excess of c itself; if v is one-tenth of c then c2/v is ten times c. There is no way by which we can observe or measure this speed, and it does not represent anything very real. So far as we are concerned it has little more significance than the speed of a shadow moving across the floor, a speed that may often exceed that of the object casting the shadow. This super-luminal speed of the de Broglie wave need give no more cause for concern than the speed of a shadow.
11.03 The conventional wave packet thus contains only imperfect information about the particle between its two nodes, but it does contain all the knowledge we can have of it until we make our next observation. Furthermore quantum theory ensures that, if we repeat an experiment many times, the probability density (based on our incomplete information) of this next node lying at any particular point within the packet, is given by |Y|2, the squared modulus of the complex wave function at that point. So while some features of this wave, the CWF of quantum mechanics, do codify information which nature uses to connect one node with another, other features are essentially subjective, and are related only to the limited knowledge which a particular person happens to have of the particle's history. It must also be time-asymmetric, for as the text books show, although the wave packet moves in a manner which we can associate with our picture of the moving particle, its size increases as it progresses, because of our uncertainty in the value of v. The real elements in such a wave, the elements which it shares with the NWF, must comprise only those features which, firstly, are independent of any individual's knowledge or lack of knowledge, and secondly, are time-symmetric.
11.04 Much of the formalism of quantum mechanics can be derived from one simple hypothesis. Let us suppose a particle of rest-mass mo
has a node whose position in space-time is A, and whose next node
occurs at B, in a region free from other neighbouring particles. We
shall represent only two dimensions on our diagram, one dimension of
space, x, and the time dimension t. We shall simplify the picture
further by viewing the situation using the reference frame in which the
particle is at rest, i.e. for which x = 0 at both A and B.
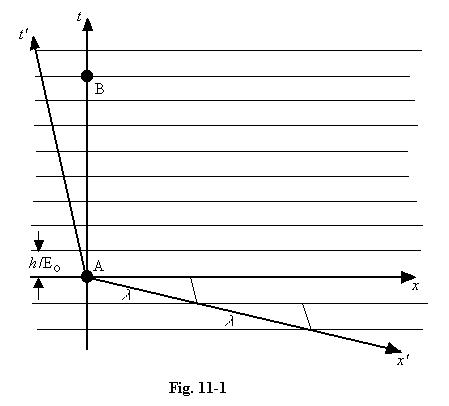
The assumption we make is that the region of space-time surrounding
such a stationary particle is filled with a uniform wave whose
frequency is given by Eo/h, where Eo = moc2, the particle's rest energy, and h is Planck's constant. The equation of the wave is therefore:
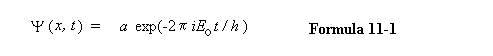
and we are proposing that this wave is, in fact, the particle's NWF. As explained in Chapter 3, this function represents a complex number, and it can be visualised as a two-dimensional vector of length a, rotating at high speed. The function contains only one variable, t, and makes no reference to the x, y or z values of space, and so it has the same value throughout all space (in this reference frame); the rotation we imagined represents the changing direction of the vector at different times t, a direction that at any instant is everywhere identical. The whole of space at each instant of time is represented in our diagram by a line parallel to the x-axis, and we have drawn lines corresponding to those times at which the phase of our wave function happens to be zero. In practice these lines would be very closely spaced, for the frequencies associated with all the common atomic particles have high values. For example, the frequency we must associate with an electron at rest is about 1020 (one hundred million million million) per second.
11.05 It
is not possible to observe this wave, but we can gain some insight into
its behaviour if we consider how it would appear to an observer moving
relative to the particle, (or what amounts to the same thing, to an
observer at rest viewing a moving particle). Let us suppose the
observer is moving with speed v along the negative x-axis. The t'
axis on our diagram shows the observer's world-line, and because
Special Relativity teaches us that such an observer will have a
different "now" plane from that of the particle, we draw his x' axis also. Notice, as always, that we must not attribute any change or motion
to this space-time diagram. But even if the diagram itself cannot
change, we might be allowed the luxury of imagining ourselves to move
steadily along the t' axis, to find out what we would observe,
with our illusory belief in a "moving" time. At any moment of time, the
events which are happening "now" lie on a line parallel to our x' axis,
and as this line moves upwards on the diagram we see its intersections
with the electron's waves moving rapidly away from us, to the right on
the diagram. Quite simple calculations, making use of the
transformations of Special Relativity (see Appendix 1), show that the
wavelength along the x' axis is given by h/mv, which is of course just l,
the wavelength as given by de Broglie's formula. Indeed de Broglie used
a similar argument in the 1920's to derive his formula, but without
realising the significance of the premise from which he started. As
shown in the Appendix, these calculations gives us the standard wave
equation for a free particle in quantum theory:

11.06 It
may be thought that the set of parallel waves described by Formula 11-1
is no more than a mathematical artefact to help us calculate the value
of l for different observers. But as its
layout and spacing depends only upon the mass of the particle, and is
independent of its velocity with respect to the observer, it is
reasonable to suppose that these waves do indeed have a real physical
existence. A set of waves similar to those illustrated is associated
with each segment of the world-line of a particle, i.e. between each
consecutive pair of nodes. This wave is independent of the observer or
his velocity, as it must be if it represents the objective NWF of the
particle. It contains sufficient information to determine the direction
in which the particle is moving (for the particle's assumed world-line
is orthogonal to the plane of the waves), its rest mass (given by Eo,
which determines the frequency), and at each moment of time, the phase
value which is needed to specify its behaviour in interference
experiments.
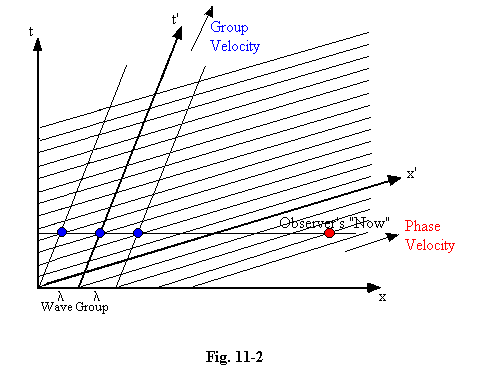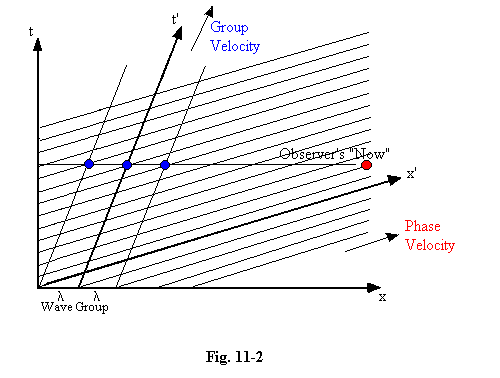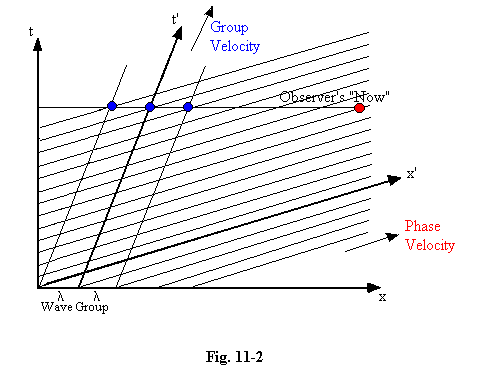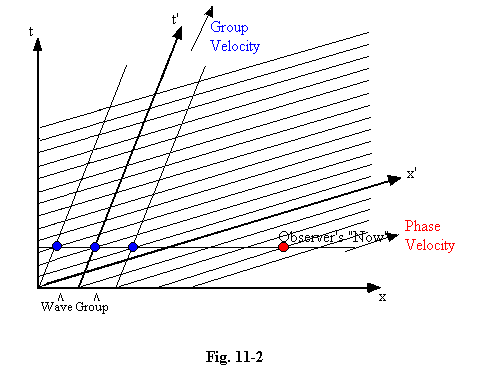
11.07 A clearer picture of what the observer can or cannot see is often presented if we draw our diagram in the observer's rather than the particle's reference frame. Here the x-t axes are the observer's, and the x'-t' axes are the particle's. We again show the parallel lines corresponding to the particle's NWF, and we show also the "wave group" or "wave packet" with which a particular observer might describe the particle's motion. The animation shows the x-axis to move steadily upwards to represent the (apparent) progression of the observer's time. (If your browser does not support animation, you must imagine this movement.) The wave packet will be seen to move along with the "group velocity" v, and the NWF waves to move rapidly through the packet, with the superluminal "phase velocity" c2/v, as the standard wave theory of quantum mechanics tells us they must. As explained above, we cannot in practice observe these waves, but by indirect means, for example in interference experiments, we can measure the wavelength, l, giving the correct value for the particle's momentum (h/l) in the observer's reference frame.
11.08 We are beginning to see which features of our conventional wave form are objectively real, and which parts are subjective. The NWF, associated throughout space and time with this segment of the particle's history, can be believed really to exist, and its form is independent of anything we choose to do. But the wave packet which we imagine to move along the x-axis is subjective, and its wavelength depends upon the observer's velocity relative to the particle. The size of the wave packet also is subjective, and in a different way; it is dependent not just on the observer's state of motion, but on the extent of his knowledge of the particle's past history. It has nothing to do with the objective state of affairs, but simply indicates the precision which our experimental arrangement allows in the measurement of the particle's past positions. And because we have access only to a restricted part, dx, of the infinite wave form, our estimate of the speed v and the wavelength l must be uncertain, as we have explained, and as decreed by the laws of Fourier analysis. In the diagram the width of the packet is about 2l, which means that any determination we attempt to make within the packet for the value of l will be in doubt by about l/2. From this we deduce that our attempt to find the particle's momentum p will be in doubt by about p/2. So dx.dp > 2l.p/2, which equals lp, or h, as we already know from Heisenberg's uncertainty principle.
11.09 So starting only with our assumption that the NWF of a particle at rest is described by Formula 11-1, we have derived several of the text-book formulae for the behaviour of a moving particle. The particle's NWF is manifest to us only when we are moving relative to that particle, and the transformation of Special Relativity ensures that our space makes a small angle with the crests of the wave function. The spacing of the intersections determines the wavelength of the waves we observe, and these appear to run along our x-axis at the expected speed as our time seems to advance. Proceeding along similar lines much of the standard quantum theory can be deduced.
11.10 So far we have considered only the NWF of an isolated particle in free space. In more complex situations the form taken by the NWF is closely related to the disposition of nodes throughout space-time, and we can picture the NWF as a superposition of the waves associated with every consecutive pair of nodes, and as permeating the whole of space-time. But it may be asked which partner of the duo, the wave or the nodes, is responsible for the other? Does the wave determine the disposition of nodes, in the same way that a country's road network determines the location of its road junctions and cross-roads? Or does it merely reflect a layout which is already decided, in the way that such a road network reflects the locations of the country's towns and villages? It seems likely that the question is really without meaning. Our usual criterion for deciding which of two events is responsible for the other is to ask which occurs first in time. Our villages must have been located before tracks were laid down to connect them, so the locations of the villages determined the layout of the tracks. But the crossroads could not exist before the roads themselves, and so their locations were determined by the layout of the roads. In each case the earlier event is responsible for the later. Such a question cannot be answered for the wave and its nodes, however, since the wave is supposed to fill the whole of space-time and so exists both before and after the events it describes. It seems that the question of dependence cannot be answered, and can be dismissed as either meaningless or, at any rate, unimportant. The whole of nature comprises a pattern of nodes distributed throughout space-time and a related network of waves which connects them. We are not to ask which of these is responsible for the other.
11.11 The NWF for a single particle, describing its "motion" from one node to the next, behaves in some respects like the CWF of traditional quantum mechanics, but with one important difference. We form the CWF from a position in which we know something about the time and position of the first node, but know little about the second one, and we can only calculate probabilities for it, using the distribution given by the squared modulus, |Y|2, of the waveform. For the NWF, on the other hand, the two nodes are on an equal footing. It "knows" the time and location of both nodes, and its form relates equally to both; no uncertainties and no probabilities are involved. But from our point of view, it is sometimes valuable to use the NWF to give us probability information. Many of the experiments we set up, such as those involving interference, concern the preparation of a large number of particles in identical states, and from a theoretical point of view the NWF can then be used to give the expected distribution of final states. There is nothing unreal about the interference patterns produced on a photographic plate, and these are related to the superposition of NWF waves in the same way as that described by conventional quantum theory using the CWF.
11.12 The
above paragraphs all refer to a particle such as an electron which can
move only at speeds less than that of light. Before we end this review
of the Nodal Wave Function we shall look briefly at the corresponding
function for particles such as photons. The NWF of these particles
cannot take the same form as that of massive particles, firstly because
their rest-energy is zero, and secondly because there is no reference
frame in which they at rest. Our approach is to assume that the Formula A,
which we obtained in Appendix 1, still applies, and then derive the
required NWF from this. The resulting formula, although it describes
the waveform in terms of the reference frame in which the particle's source is at rest rather than the particle itself, and quotes the wavelength l
applicable only to this frame, nevertheless is frame-invariant. The NWF
of such massless particles is derived in Appendix 2, and is as follows:
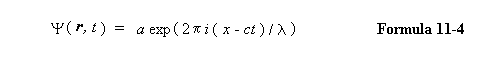
These particles display different wavelengths, energy and momenta in different frames of reference, just as do massive particles, but the frequency of the oscillations which they display also assumes importance in this case, and is often observable. Indeed ordinary radio waves take this form, and we generate them by means of familiar electrical circuitry designed to produce the required frequency. The formula, and the diagram, both show that the observed frequency is c/l in the reference frame where the wavelength is l, as we should expect.
11.13 It may seem strange at first sight that the wavefronts do not intersect the particle's trajectory, so that Y seems to have the same phase along the whole trajectory, but a little thought confirms that this must indeed be the case, for the relativistic time dilation effect of a particle moving at the speed of light becomes infinite; a clock moving with the particle registers the passage of no time at all between the beginning and the end of its flight. The phase of the Y-value is the same at the point of emission and at the point of absorption.
11.14 We should mention briefly the way the NWF of a particle can give rise to interference effects. The NWF of a particular particle can interfere only with itself, as when two adjacent parts of the wave become separated and subsequently come together, so that their Y values become added, or superposed. The wave of one particle does not interfere with that of another, but there are circumstances in which the NWF corresponding to one segment of a particle's history can become superposed on that from another segment to produce interference effects. This can happen, for example, when a particle traversing Young's apparatus collides with a low energy photon at one of the slits. We saw in Chapter 6 that the particle can still go on to produce interference effects, provided the photon's energy is low enough, so that the values carried by the wave-form in the next segment of the particle's history are almost identical with its previous values. It behaves almost as if no collision had occurred, and contributes to the interference in the same way in both cases. The interference takes place between two different segments of the particle's wave form, one having passed without interruption through the first slit, and the other resulting from the photon collision at the second one. We discussed another example of this phenomenon in Chapter 7, where one branch of a divided wave form is reflected from a mirror, and suffers a collision there, and yet can still go on to interfere with the other branch which has suffered no collision.
11.15 We
shall give just one illustration of the way a diagram like that above
can help us solve problems involving the NWF of a photon. Let us
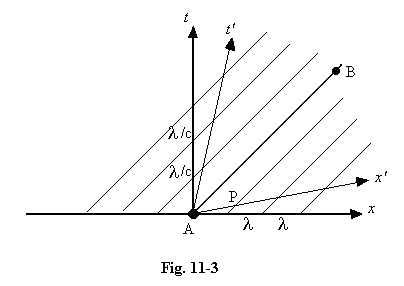
suppose an observer is moving along the x-axis ahead of the photon with speed v
relative to its source, and that it overtakes him at B. If he measures
the wavelength of the photon, he will obtain a value greater than l because of the Doppler effect. We have drawn the x' and t' axes for the observer, and it can be seen that the measured wavelength, AP, is in fact greater than l,
as we expect. To keep the diagram simple we have centred the observer's
axes on the point A where the particle is emitted, but the measured
wavelength would be the same length AP wherever it had to be taken, and
whatever method was used. In Appendix 2 we give the necessary
mathematics to calculate the length of AP, and we obtain the result:
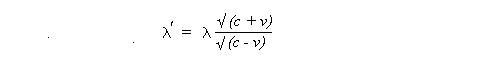
which relativity theory tells us is the correct value of the Doppler shifted wavelength for an observer receding from a source of light with wavelength l. As in the case of subluminal particles, our postulated description of the NWF of the massless particles can lead to many of the fundamental features of quantum theory.
11.16 Throughout this chapter we have referred only to the NWF of elementary particles such as electrons or photons, but many experiments prove that interference effects can be observed also with composite bodies such as atoms and molecules. Whole atoms have been used in particle experiments for several years, and at the time of writing quite large molecules are beginning to show that they also are capable of demonstrating interference. Does this imply that such bodies have their own NWF, or can the observed effects be explained in terms of the wave functions of their individual elementary parts?
11.17 The behaviour of an unconnected group of particles differs greatly from that of a composite body because of the strong forces which bind together the components parts of such a body. A photon striking an isolated electron affects only that electron, and in particular can change its momentum, while a photon striking an electron in an atom, provided it is not sufficiently energetic to shift the electron to a higher energy level within the atom, must change the momentum of the atom as a whole. The internal forces which hold the electrons in their place around the nucleus, are sufficiently powerful to maintain the configuration of the atom, so that it rebounds as a whole. Today we picture these internal forces as being transmitted by "virtual" photons or other "messenger" particles, and these must have their own NWF's to convey information between each pair of nodes, and in particular to transmit any change of momentum to the atom as a whole. But these effects are purely internal, and none of the local wave functions can reflect the momentum of the atom as a whole. So it seems certain that every atom, every molecule, or indeed every rigid body, must have its own NWF which carries information about the body's momentum, and which under suitable conditions can be responsible for interference effects.
11.18 If a group of discrete particles happen all to be moving with the same direction and speed, each will behave as if the others were not present. When such a group encounters an obstacle, such as a diaphragm containing a narrow slit, each particle will be diffracted as if it were alone. Its wavelength is related to its momentum according to de Broglie's formula, and those with less momentum will tend to be diffracted through greater angles because of their greater wavelength. But if these particles are locked together, as are the electrons in the shells of an atom, or the component atoms of a molecule, and this composite body survives its encounter with the diaphragm, then it is diffracted as a whole. Its momentum is obviously greater than that of each component, and so its wavelength is less, and its mean angle of diffraction will also be less. This explains in part the fact that we do not normally see interference effects in everyday life; other things being equal, the larger a body the smaller is its wavelength, and the more difficult is it to devise apparatus which will reveal it. An object such as a bullet or a pea, travelling at the sort of speed with which we are familiar, has a de Broglie wavelength many orders of magnitude smaller than any apparatus we could devise to reveal diffraction or interference effects.
11.19 One can easily imagine why the individual particles of such a composite body do not themselves give rise to interference effects. Each particle is kept in its place by the constant buffeting of the virtual photons which hold the body together, each collision being represented by a node, and causing some change in the particle's momentum. So if the body as a whole has two or more routes to a destination, as for instance in a two-slit experiment, the separate particles have no chance of preserving their coherence, just as a stream of unconnected particles produce no interference if they suffer collisions during their journey through Young's apparatus.
11.20 It is less easy to understand why the composite body is associated with a wave of its own, which under suitable conditions can itself display interference effects. The wave is in no sense a sum of the Nodal Wave Functions of the component particles. The essential defining characteristic of a NWF is its frequency, which we have shown is given by moc2 / h, so that the frequency of the body as a whole is in fact the sum of the frequencies of its components, but this has no mathematical significance. Furthermore we have shown that the NWF of one particle never interacts with that of another. But interestingly the actual NWF of the whole body is the product of the component NWF's, for each NWF is given by exp(-2pimoc2t / h), and the exponential of a sum of exponents is the product of the exponentials of the individual exponents (or in symbols, exp(x+y) = exp(x).exp(y) ).
11.21 There is no obvious reason for this to be the case, and at present we must accept it as an unexplained fact that every composite body is associated with its own de Broglie's wave, just as is every fundamental particle. Indeed there is much which is not understood in this area. From the point of view of traditional quantum theory there are three correlations for which no explanation is known. The classical quantum physicist must accept without question that (i) every particle has a characteristic mass, which is additive when such a particle has component parts, (ii) that the magnitude of the effect produced when a body collides with another is determined by its momentum, and so is proportional to its mass, and (iii) that the de Broglie wavelength of a particle (as seen by an observer moving relative to the particle) is inversely proportional to its mass. Feynman understood clearly the depth of our ignorance of the true significance of mass. He wrote in 1985:
... there remains one especially unsatisfactory feature: the observed masses of the particles, m. There is no theory that adequately explains these numbers. We use the numbers in all our theories, but we don't understand them -- what they are, or where they come from. I believe that from a fundamental point of view, this is a very interesting and serious problem. (QED, p.152)11.22 The Nodal Theory has one less problem to solve than has traditional quantum theory, for it denies the existence of the particles themselves. The "mass" of a body, and the Nodal Wave Function of such a body, do not need separate explanations, for mass is no more than the frequency of the wave. But nodal theory still has no explanation to offer for the remaining two questions, of why the wave frequency of a composite body can be found by adding the frequencies of its parts (or equivalently, why the NWF itself is found by multiplying NWF's), and why the magnitude of the effect of one body on another is proportional to this frequency. We know that the world-line of every composite body corresponds to a wave in space-time which we can describe exactly, but we lack totally any understanding of why this should be so. In this respect such bodies do not differ from the elementary particles of which they are composed, for again we know precisely the parameters of the NWF joining the nodes of such particles, but can give no explanation for the wave, or account for the values of its parameters.
(c) Hector C. Parr (2002)
Previous Next Home Hector Parr's Home Page