Ch. 1
Ch. 2
Ch. 3
Ch. 4
Ch. 5
Ch. 6
Ch. 7
Ch. 8
Ch. 9
Ch.10
Ch.11
Ch.12
App.1
App.2
App.3
Biblio.
Index
Hector Parr's Home Page
Quantum Physics: The Nodal Theory
Hector C. Parr
Chapter 1: Preview
1.02 But while we enter the twenty-first century with unprecedented skills in manipulating the natural world, we have no generally agreed understanding of why our methods work. Most scientists engaged in research or development in this field will seldom need to think about the philosophical basis for the techniques they use, but those who do are still confronted with problems and paradoxes of a type with which the human mind has never before had to grapple. Several imaginative solutions to these problems have been suggested, but each involves ideas which are difficult to accept, and not one of the proposed interpretations seems wholly satisfactory.
1.03 The greatest thinkers of the twentieth century, among whom we include Albert Einstein, Niels Bohr, Werner Heisenberg and Richard Feynman, always wrote and spoke with great clarity. They were particular over their choice of words, and careful not to let their fascination with the new phenomena lead them to exaggerate the strangeness of the world they were exploring. But unfortunately some of their colleagues were not blessed with the same clear vision or lucidity of expression, and their writing sometimes lacks the precision which is essential if they are to present the mysteries of the quantum world without leaving conceptual gaps into which others can stumble. The problems are so baffling that it would not be fair to blame our failure to resolve them on any individuals, but it does seem likely that the rather slack writing of some commentators, and their tendency to sensationalise the unexpected nature of the effects they describe, has retarded the search for an acceptable philosophy.
1.04 Soon after the start of the twentieth century it was realised that, in the atomic domain, things which had been assumed to be particles, such as electrons and atoms, often manifested themselves as waves, and conversely things like light, which we had taken to be electromagnetic waves, sometimes behaved as if they consisted of particles, which were given the name "photons". This strange duality, and the real nature of these waves and particles, presented a problem which seemed to become more rather than less obscure as our knowledge increased, and now a century later, is far from being fully understood. Much of the discussion and disagreement has centred on the nature and effects of measurement in the quantum world, and the so-called "collapse of the wave function" which appears to occur whenever a measurement or an observation is made of a quantum system. It is here in particular that careless choice of words can exacerbate a problem rather than illuminate it. A particle cannot be observed or measured without disturbing it to some degree. The same principle applies when making macroscopic measurements, for instance in electrical circuits where any measurement of the current flowing through a circuit element necessarily affects the voltage across it, and vice versa, but whereas these effects can be minimised to any extent by careful design of experiments, in the quantum world there is a natural lower limit to the level of disturbance that must be tolerated because of the quantised nature of energy. The apparatus we set up to measure or observe something in the atomic world necessarily affects the quantity we are measuring to a degree we cannot predict or reduce.
1.05 The Institute of Physics which Niels Bohr established at Copenhagen in the early 1920's became the chief centre at which these matters were discussed, and many of the greatest physicists of the day visited Bohr there and contributed to the deliberations. The "Copenhagen Interpretation" which Bohr and his friends thrashed out in these early days is still regarded by many observers as the authoritative explanation of the quantum paradoxes, but this interpretation leaves many questions unanswered, and indeed seems to mean something different to almost every writer who describes it. Bohr appeared to insist that we should talk about the behaviour of waves or particles only in relation to particular types of observation or experiment, and that it was meaningless to discuss their "reality" in general terms. But on this matter Bohr's view was strongly opposed by Einstein. Throughout his life Einstein maintained a belief in the "real" existence of particles in all circumstances, and the doubts which quantum theory had to throw on this reality, he maintained, indicated that the theory was wrong, or as Einstein expressed it, charitably, was "incomplete".
1.06 Niels Bohr in his writings made it clear that in talking about an "observer" causing the collapse of a wave function he was referring merely to the apparatus involved, and attached no importance to whether a human was actually aware that an observation had been made. The collapse was brought about by "irreversible amplification effects" such as the production of marks on a photographic plate, or the "building of a water drop around an ion in a cloud-chamber". And Werner Heisenberg, writing in 1958, explains that, in its later form, the Copenhagen Interpretation envisaged this wave function to be partly subjective, containing information about our knowledge of a system as well as information about the system itself.
This probability function represents a mixture of two things, partly a fact and partly our knowledge of a fact. ...It should be emphasised, however, that the probability function does not in itself represent a course of events in the course of time. It represents a tendency for events and our knowledge of events. (The Copenhagen Interpretation of Quantum Theory, ch.3)1.07 But this uncontentious portrayal of the wave function (Heisenberg's "probability function"), as it was passed from one commentator to another, became more and more sensational and outlandish. Paul Davies is one of the more rational writers on scientific topics, and yet he could write in 1987,
So long as a quantum system is not observed, its wave function evolves deterministically. In fact, it obeys a differential equation known as the Schrodinger equation (or a generalisation thereof). On the other hand, when the system is inspected by an external observer, the wave function suddenly jumps, in flagrant violation of Schrodinger's equation. The system is therefore capable of changing with time in two completely different ways:one when nobody is looking and one when it is being observed. (The Cosmic Blueprint, p.168).John Wheeler goes further in attributing supernatural powers to the human observer:
The quantum principle shows that there is a sense in which what the observer will do in the future defines what happens in the past -- even in a past so remote that life did not then exist, and shows even more, that 'observership' is a prerequisite for any useful version of 'reality' (Quoted by Paul Davies in Other Worlds, p.126).And according to Davies, Eugene Wigner takes us yet further along this road;
It is not enough to equip the laboratory with complicated automatic recording devices, video cameras and the like. Unless somebody actually looks to see where the pointer is on the meter (or actually watches the video record), the quantum state will remain in limbo. (The Ghost in the Atom, p.31).Bohr would certainly not have approved of some ideas which have been attributed to him by more recent popularisers of quantum physics. We read,
The strangest thing about the standard Copenhagen interpretation of the quantum world is that it is the act of observing a system that forces it to select one of its options, which then becomes real. ... What’s worse, as soon as we stop looking at the electron, or whatever we are looking at, it immediately splits up into a new array of ghost particles, each pursuing their own path of probabilities through the quantum world. Nothing is real unless we look at it, and it ceases to be real as soon as we stop looking. (In Search of Schrodinger’s Cat, John Gribbin, 1984).1.08 Such provocative writing may help to sell popular science books, but has done nothing to advance the understanding of quantum physics. Contrast it with Bohr’s cautious approach to the problem of observing quantum phenomena;
... I warned especially against phrases, often found in the physical literature, such as ‘disturbing of phenomena by observation’ or ‘creating physical attributes to atomic objects by measurements’. Such phrases, which may serve to remind of the apparent paradoxes in quantum theory, are at the same time apt to cause confusion, since words like ‘phenomena’ and ‘observations’, just as ‘attributes’ and ‘measurements’, are used in a way hardly compatible with common language and practical definition. (Discussions with Einstein, 1949)1.09 But the ultimate accolade for eccentricity must go to Hugh Everett. Here is Davies' explanation of Everett's "many worlds" theory:
... if a quantum system is in a superposition of, say, n states, then, on measurement, the universe will split into n copies. In most cases n is infinite. Hence we must accept that there are actually an infinity of "parallel worlds" co-existing alongside the one we see at any instant. Moreover, there are an infinity of individuals, more or less identical with each of us, inhabiting these worlds. (The Ghost in the Atom, p.35)Paul Davies himself, however, can bring us down to earth again, for just a few pages beyond the passage quoted above, in which he attributes different behaviour to a system according to whether or not someone "is looking", he gives us this much more reasonable assessment:
The wave function represents not how the system is, but what we know about the system. Once this fact is appreciated, the collapse of the wave function is no longer so mysterious, because when we make a measurement of a quantum system our knowledge of the system changes. (The Cosmic Blueprint, p.172).
1.10 The belief held by some physicists that their own conscious awareness of a measurement somehow affects the particles in the physical world which have been observed, appears to have arisen only because of careless (or sensational) statements about the measuring apparatus having such an effect on those particles. It is then just a short step to believing that the wave function which collapses when it knows a measurement has been made, is itself a part of the system being observed, rather than a description of the physicists' own thought processes, and that its collapse is a physical change in the system brought about by the observer's changed perception of it.
1.11 Further examples of bad reporting can be found in the many descriptions of the "Heisenberg Uncertainty Principle". Heisenberg showed that, if we try to measure simultaneously the position and the velocity of a particle, then there is an essential uncertainty in one or both of our measurements. It is more convenient to express this fact not in terms of the particle's velocity, but of its momentum, which is found by multiplying the velocity by the particle's mass. Then Heisenberg tells us that the uncertainty in the position multiplied by the uncertainty in momentum must always exceed h, Planck's constant. (This small number plays an important part in Quantum Mechanics, and its value is known accurately.) Other writers tell us less formally that "it is impossible to know both the position and the momentum of a particle". But such a statement is not nearly good enough; under what circumstances does it apply? Does it refer to the position and momentum at some time in the past, in the present, or the future? Does it concern the values of these variables at the moment a particle is emitted, at the moment it is detected, or at some time in between? The writers do all agree that there is no fundamental restriction on the accuracy with which we can measure the time and position of the emission of a particle, or of its detection by a measuring device, provided we do not at the same time try to find out anything about its momentum or its energy. But for a particle in free space, where we can assume it moves in a straight line at constant speed, if we know the place and time at both ends of its track, we can calculate the particle's velocity (to whatever degree of accuracy our methods allow) by simply dividing the distance travelled by the time taken. This gives us the momentum, again with a degree of accuracy limited only by our experimental techniques, and not by fundamental restrictions of the uncertainty principle. As usual, Richard Feynman can be trusted to describe the situation clearly. He writes,
It is quite true that we can receive a particle, and on reception determine what its position is and what its momentum would have had to have been to have gotten there. That is true, but that is not what the uncertainty relation refers to. This equation refers to the predictability of a situation, not remarks about the past. (Lectures on Physics III, 1965, Addison-Wesley).We see that Heisenberg’s rule may not apply to past trajectories of a particle. But careful examination of situations in which the position-momentum uncertainty relationship does apply is revealing. The simplest case occurs when a collimated beam of particles is projected onto an opaque screen with a small hole in it, and they appear to be deflected from a straight course by diffraction. Those particles which pass through the hole have a well-defined position here, and this entails a random change of momentum in accordance with the Heisenberg rule, so that we cannot predict the subsequent direction of a particle's trajectory. Notice that in this case we know the particle's position not because we have observed it there, but by "default" or "selection". Most of the incident particles do not pass through the hole, for they collide with the screen, and our experiment does not reveal the positions of these collisions. But the small selection of particles which do go through the hole have a known position simply because they have not collided with the screen. It appears, therefore, that uncertainty arises only when we are interested in the position and the momentum of a particle between two collisions, or at one collision without using information we could gain from its previous one. If we know the time and position of a consecutive pair of past collisions we may well be able to determine the momentum between the collisions without the restrictions of the uncertainty relation. This is not made clear in many of the written accounts of the principle.
1.12 A crucial fact that is often forgotten is that a particle can have no direct effect on another particle unless it collides with it, or unless a third particle such as a photon travels from one to the other. (Notice that, when two particles are described classically as attracting or repelling one another, a quantum description can always be given in which the influence is transmitted via third particles, such as photons or gravitons.) It follows that a particle can have no influence whatsoever on anything else between one collision (or emission) and the next one. Any apparatus we set up to observe or to measure a particle must necessarily involve a new collision with that particle. The only information we can gain in the absence of such a collision must be by default. This simple truth is the basis for the new attempt which the writer makes on these pages to resolve the difficulties surrounding quantum mechanics without undue threat to credibility; he calls this approach the Nodal Interpretation, and will present its main features in the following chapters.
1.13 Let us take as a starting point the strange fact that, because you can know nothing at all about a particle between one collision and the next, you can assert anything you like about its trajectory and no-one can prove you wrong. What the Nodal theory asserts is that a particle does not exist between collisions. The universe consists not of particles, but just of those events which we have come to regard as collisions between particles, together with the wave functions which connect these collisions, and pass information between them. We call these events nodes, and we shall examine in later chapters what properties they must possess if we are to explain all quantum phenomena in terms of nodes alone. The particle does not travel from node to node, but there is a sense in which information connects the nodes to each other, and some sort of wave function carries this information. In chapter 11 we examine in detail the nature of this wave function, and discover in what respects it resembles the wave function of traditional quantum theory.
1.14 Just as a foretaste, consider how this theory deals with the well-known two-slit experiment, in which a beam of monochromatic light passes through two slits in an opaque screen, and is seen to produce an interference pattern, consisting of alternate dark and light bands, when the divided beam falls onto a photographic plate. This was easily explained by nineteenth century physics, for light was then believed to consist of electromagnetic waves, and because the two routes to any particular point on the plate can differ slightly in length, the two waves may be in phase or out of phase; they are said to "interfere". Where they are in phase they reinforce each other, and a bright band results, but where they are out of phase they can neutralise each other and give a dark band. What is far more difficult to explain is that the experiment can be repeated with a beam of particles such as electrons instead of light rays, and is found to give a similar pattern of light and dark bands. How can this arise, when interference is essentially a property of waves, and not of particles? Feynman described the phenomenon as being at "... the heart of quantum mechanics. In reality, it contains the only mystery" (The Feynman Lectures III, 1965). When a single particle traverses the apparatus it must "know" it has to avoid certain areas of the screen, namely those in the dark fringes, but only if both slits are open. If one slit is closed no interference pattern is produced; so closing one slit can increase the number of particles arriving at points within the dark areas. We ask how the particle can know whether the slit through which it has not passed is open, or whether, perhaps, the particle splits in half and passes through both slits. But a simple consideration of the masses of the two parts, and their corresponding wavelengths, shows that this last suggestion cannot be the true explanation, and it has become fashionable for popular writers on quantum theory to talk about particles being "in two or more places at the same time". This unsatisfactory description was put on a more formal footing in the early 1930's when Paul Dirac wrote about the "Principle of Superposition of States", and formulated an ingenious mathematical treatment of the idea. He describes the situation in which a particle apparently passes through two slits at the same time as a "superposition" of the two separate states in which it passes through one or other of the slits. Dirac writes:
The nature of the relationships which the superposition principle requires to exist between the states of any system is of a kind that cannot be explained in terms of familiar physical concepts. .... The intermediate character of the state formed by superposition thus expresses itself through the probability of a particular result for an observation being intermediate between the corresponding probabilities for the original states, not through the result itself being intermediate between the corresponding results for the original states. (The Principles of Quantum Mechanics, Pp.12-13).
1.15 Dirac's thorough treatment, and the special notation he developed to represent quantum states and their superpositions, have formed the basis for the mathematics which practical workers in the field of particle physics have used with notable success throughout most of the twentieth century. However, they provide little help for those wanting a clear picture of the natural processes lying behind the mathematics, and it is hoped the Nodal theory might help to fill this gap. Briefly, the new theory denies that a particle exists at all while traversing the "two-slit" apparatus, so it passes through neither slit. We do not need to believe it can be "in two places at once". A full description of our analysis of this experiment will be found in Chapter 6.
1.16 There is one other principle to which some writers on quantum mechanics pay lip-service, but fail to pursue to its conclusions, and which we must develop to understand fully the Nodal theory. It is known that all quantum processes, when considered as the interactions of particles (with one trivial exception) are time symmetric. If time were considered to "flow" in the opposite direction, all fundamental processes would still be in accordance with the rules of quantum mechanics; we would not be able to detect, by watching the behaviour of sub-atomic systems, which way time was flowing. (This would not be true, of course, if we were observing macroscopic processes, such as bombs exploding, water flowing, or cars colliding, for almost all such processes are dominated by the asymmetrical second law of thermodynamics.) It follows that any description of interactions on the microscopic scale should also be time symmetric, and all the popular quantum philosophies fail this test. The collapse of the wave function, which most of these philosophies involve, is clearly an irreversible process, and so, a fortiori, would be the continual splitting of the universe into more and more copies of itself, which the Everett interpretation requires. This is a simple test which we can apply to any description of quantum phenomena, and which eventually we shall apply to the Nodal theory. If our picture becomes less plausible, or if it changes in any fundamental way, when time is considered to “flow” in the opposite direction, then our description is faulty.
1.17 Again, we shall quote
just one simple example of this principle of reversibility, and leave
fuller discussion for later chapters. When a randomly generated stream
of photons strikes a polarising filter, such as a sheet of
Polaroid, it is found that one half of them pass through it, and one
half are stopped. But if a second filter is placed behind the first,
and if the optical axes of the two filters are parallel, every one of
the photons which passes through the first polariser passes also
through the second. If the axes of the two polarisers are not parallel,
a simple formula tells us what proportion of the photons passing
through the first filter pass also through the second. [If the angle
between the optical axes of the two filters is q, then this proportion is known to be cos2q.]
These facts are explained, in traditional quantum theory, by assuming
that each photon has its own axis of polarisation, and that when a
photon strikes a polariser, this same formula tells us the probability
that it is transmitted. Those that are transmitted are supposed to have
their own axes shifted so that they then become parallel to the optical
axis of the polariser through which they have passed. The very act of
passing a photon through a polariser, we are told, constitutes a measurement of the photon's axis, so we should not be surprised that it has an instantaneous effect on that photon.
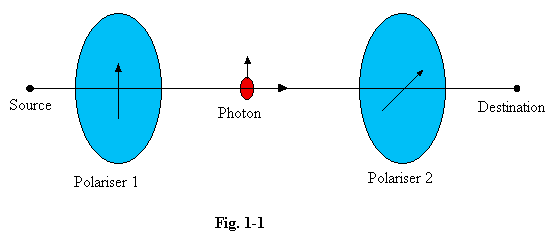
1.18 Let us consider the possible outcomes when we try to pass a stream of photons through two such filters with their axes at some definite angle, say 60o, as illustrated here. One half of them are stopped by the first filter, and three quarters of the remainder are stopped by the second. If we concentrate on a single photon which passes through both, let us imagine what it looks like when between the two filters. Since it has just passed through the filter on the left, its axis must be vertical, as shown. We might prepare a little "movie" of the process, to show our students what we think happens. But suppose we accidently show the movie in reverse. The photon firstly passes through the right hand filter, and so its axis should then be at an angle of 60o as shown in the second diagram, and yet we can see clearly that it is not, it is vertical.

So by looking at our movie we can tell which way time is "flowing", in breach of our principle of reversibility. In the nodal picture this problem disappears, for the photon does not pass through the filter at all; it exists only at its source and at its destination, on the right or left as the case may be, and not at any points in between. Note carefully that a photon which is not transmitted by a polariser does have a collision there, and so does exist as a node at that point, but we are considering only the photons which have a collision at neither polariser. Of course the presence of the polariser affects the future behaviour of the photon, and we must take it into account in calculating the relevant probabilities. But the Nodal theory claims that nothing physically significant passes through the two polarisers, and so no meaning can be assigned to the orientation of the particle's axis there, and the apparent time asymmetry is seen not to exist. It may be argued that, even from the Nodal viewpoint, the wave function must pass through the two filters. But the wave function is no more than the information which is exchanged between nodes, and it is fundamentally impossible to gain access to this information except at the nodes themselves, or by introducing extra nodes, which will change the very information we are hoping to observe. The wave function must take cognizance of any polarisers in its path, but we can observe only the nodes, and the behaviour we see does not depend upon the direction in which we imagine time to be flowing. This is the viewpoint which will be developed throughout the following chapters.
1.19 The above discussion illustrates one of the greatest difficulties in understanding quantum processes, that of untangling them from our deep-rooted intuitions concerning the flow of time and the true nature of past and future, intuitions which are firmly ingrained in our thinking, but in several respects are false. We devote the next chapter of the book to this question.
(c) Hector C. Parr (2002)
Previous Next Home Hector Parr's Home Page